well, 2 ideas here:
one could generate a heightmap from x and y curves, like in this silly drawing:
and the resulting intensity distribution would be simply the outer product of the curves:
Mat intensity = curve_x * curve_y.t();
(and that's also where the 2d splines are back !)
-------------------------------------------------------
but also, your background noise is basically a gaussian distribution. (or maybe a mix of gaussians), so probably a simple mouse painting tool (where you subtract such blobs on every click) might do the trick already:
#include<opencv2/opencv.hpp>
#include<iostream>
using namespace cv;
using namespace std;
Mat gauss_blob(int siz, float sig) {
Mat k = getGaussianKernel(siz*2+1, sig, CV_32F);
return k*k.t();
}
int border=800; // max kernel size
int t_int = 220;
int t_sig = 200;
int t_siz = 100;
Mat img;
void on_mouse(int e, int x, int y, int s, void*) {
if (e==1) {
Rect r(border+x-t_siz, border+y-t_siz, 2*t_siz+1, 2*t_siz+1);
Mat patch(img,r);
Mat blob = gauss_blob(t_siz, float(t_sig)/10);
patch -= t_int * blob;
}
if (e==2) ;// r-click, *add* the blob for undo.
}
int main(void) {
img = imread("stars.png", 0);
img.convertTo(img, CV_32F, 1.0/255);
// make sure we stay inside the image
Rect show(border,border,img.cols,img.rows);
copyMakeBorder(img,img,border,border,border,border,BORDER_CONSTANT,Scalar(0));
namedWindow("gauss");
createTrackbar("size", "gauss", &t_siz, 800);
createTrackbar("sigma", "gauss", &t_sig, 800);
createTrackbar("intensity", "gauss", &t_int, 500);
setMouseCallback("gauss", on_mouse);
while(1) {
imshow("gauss", img(show));
if (waitKey(5) == 27) break;
}
return(0);
}
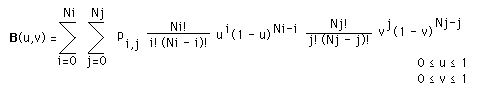
no opencv does not have any splines (or any curve-fitting, which is probably more close to what you wanted.)
also note, that the control points for splines are NOT point coords to be approximated (apart from the 1st and last). i just saw this
https://en.wikipedia.org/wiki/Curve_f...
The easiest curved line is the Bezier curve:
https://en.wikipedia.org/wiki/Bézier_...
It takes 3D points and interpolates between them. I once used Bezier curves to visualize the quaternions as they are operated on, using Z = Z*Z + C as the iterated equation. If you perform intersection of the curve and the quaternion fractal's surface, you can get a normal (derivative) at the intersection point.
Thanks for the helpful replies. I'm surprised that OpenCV has no built in functions for this. I've seen mention of correcting camera spatial distortion, so I thought this would be related.
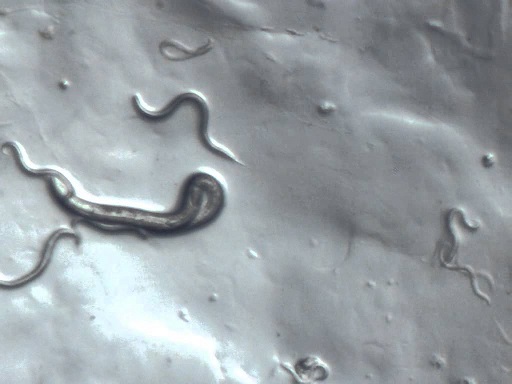
OpenCV does have adaptive thresholding, but that goes wrong in areas where there are no foreground objects for contrast. It will detect the more pronounced areas of noise as foreground.
I ran across a good illustration of what I'm looking for in the long run. This shows removal of 'curved' background illumination for a telescope image: http://help.imageanalyst.net/workflow...
Unfortunately, that's a specialized commercial program. And I'm looking for something that could adapt to more complex 2D 'light curvatures.' That's why I had envisioned a spline. But perhaps there are other approaches.
You could accelerate the light (bend the light's natural, inertial path) using gravitation. Don't forget that the bending of light's path (the bend angle) is double when using General Relativity, versus the old Newtonian gravitation. Not that it makes much difference, but you might as well try to do it right the first time.
http://www.einstein-online.info/spotl...
Thanks for the suggestion. I'm not actually working with telescope images. The link illustrated something similar as far as light/illumination correction. It sounds like you're referring to spatial distortion, which I don't need to handle in this case. I have a background field with irregular illumination, somewhat like the telescope image but often more complex. If I could find the general 2D curve for the illumination, I could subtract it to even out the image. Easier said than done.
Yes, good luck. :) And spatial distortion (curvature) only explains Newtonian gravity. The addition of time curvature is what makes GR more like reality.
^^ k,k, enough ... ;)
@Martian, so the whole talk about splines was pretty misleading. maybe you can show an example image of your problem,and what you're trying to achieve ?
that's probably, what the question should have been.
Hi Berak, The link that I posted is probably a good example: http://help.imageanalyst.net/workflow... But in this case, instead of telescopes, it's microscopes. Same problem though---irregular illumination, but with variations, like haze or filmy looking areas that sometimes gets misinterpreted as objects.
I didn't think I'd find a specific solution to this so I thought I might be able to 'roll my own' with the spline code.