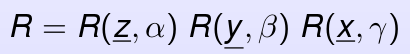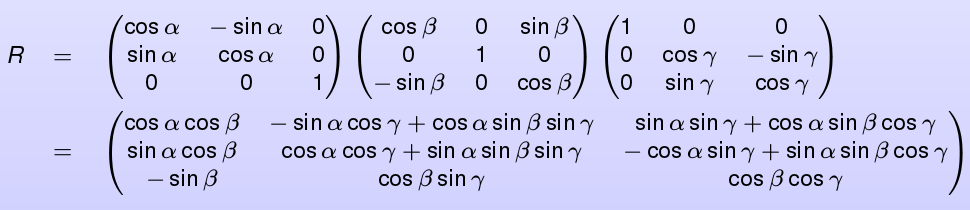I answer to the post of @Nepolo:
UPDATE 2015.07.06 -----UPDATE
2015.07.06------- UPDATE 2015.07.06
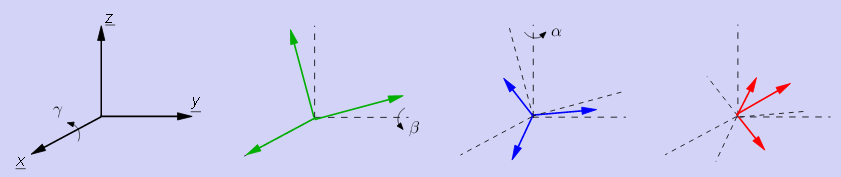
Let alpha, beta and gamma the yaw, pitch and roll angles as defined here (slide 50, Bernard BAYLE), also called Tait-Bryan angles Z1Y2X3:
The final rotation matrix can be calculated as the the matrix resulting of the multiplication of the 3 rotation matrices about each axis:
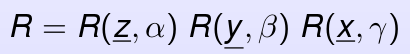
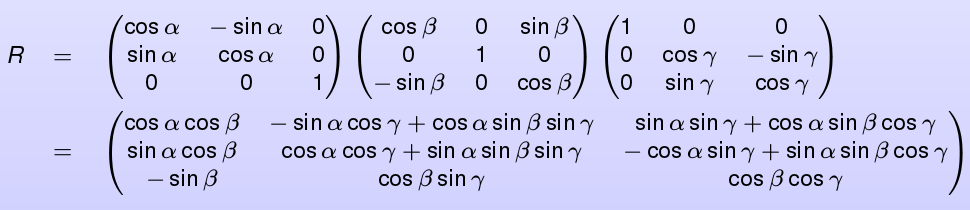
Your resulting rotation matrix is decomposed as:
cout << Qx.t()<<endl;
//RESULT
//[1, 0, 0;
// 0, 0.9999999980133975, 6.303336619882133e-05;
// 0, -6.303336619882133e-05, 0.9999999980133975]
cout << Qy.t()<<endl;
//RESULT
//[0.9999999997416501, 0, 2.273102883446428e-05;
//0, 1, 0;
//-2.273102883446428e-05, 0, 0.9999999997416501]
cout << Qz.t()<<endl;
//RESULT
//[0.985944918764345, -0.1670706951047037, 0;
//0.1670706951047037, 0.985944918764345, 0;
//0, 0, 1]
We have Qx == identity (more or less), Qy == identity (more or less) and alpha_angle=atan2(0.1670706951047037, 0.985944918764345) but you cannot end up with:
That should be the correct values Roll
5° Pitch 0° Yaw -45°
Some test code:
#include <iostream>
#include <opencv2/opencv.hpp>
cv::Mat rotationMatrixX(const double angle) {
cv::Mat Rx = (cv::Mat_<double>(3, 3) << 1.0, 0.0, 0.0,
0.0, cos(angle), -sin(angle),
0.0, sin(angle), cos(angle));
return Rx;
}
cv::Mat rotationMatrixY(const double angle) {
cv::Mat Ry = (cv::Mat_<double>(3, 3) << cos(angle), 0.0, sin(angle),
0.0, 1.0, 0.0,
-sin(angle), 0.0, cos(angle));
return Ry;
}
cv::Mat rotationMatrixZ(const double angle) {
cv::Mat Rz = (cv::Mat_<double>(3, 3) << cos(angle), -sin(angle), 0.0,
sin(angle), cos(angle), 0.0,
0.0, 0.0, 1.0);
return Rz;
}
cv::Mat yawPitchRollToRotationMatrix(const double roll, const double pitch, const double yaw) {
cv::Mat Rx = rotationMatrixX(roll);
cv::Mat Ry = rotationMatrixY(pitch);
cv::Mat Rz = rotationMatrixZ(yaw);
return Rz*Ry*Rx;
}
double rad2deg(const double rad) {
return rad*180.0/CV_PI;
}
double deg2rad(const double deg) {
return deg*CV_PI/180.0;
}
int main(int argc, char **argv) {
double roll = deg2rad(5.0);
double pitch = deg2rad(0.0);
double yaw = deg2rad(-45.0);
cv::Mat R = yawPitchRollToRotationMatrix(roll, pitch, yaw);
std::cout << "R=" << R << std::endl;
cv::Mat mtxR,mtxQ;
cv::Mat Qx,Qy,Qz;
cv::Vec3d e;
e= RQDecomp3x3(R, mtxR,mtxQ,Qx, Qy, Qz);
std::cout << "Euler angles (Roll-Pitch yaw angles) in degree=" << e << std::endl;
return 0;
}
and the corresponding output:
R=[0.7071067811865476, 0.7044160264027586, -0.06162841671621935;
-0.7071067811865475, 0.7044160264027587, -0.06162841671621935;
0, 0.08715574274765817, 0.9961946980917455]
Euler angles (Roll-Pitch-Yaw angles) in degree=[5, 0, -45]
 http://www.bilder-upload.eu/show.php?...
http://www.bilder-upload.eu/show.php?... http://www.bilder-upload.eu/show.php?...
http://www.bilder-upload.eu/show.php?... http://www.bilder-upload.eu/show.php?...
http://www.bilder-upload.eu/show.php?...