Heavy shearing effects using Hartley's rectification
I'm using stereoRectifyUncalibrated, OpenCV implementation for Richard Hartley's rectification algorithm. The problem is I'm observing shearing in one of the rectified images and it's causing problems on disparity computation.
Consider these two input images (the points pairs were produced using SURF):

Hartley's algorithm produced these two rectified images:

The epipolar lines look fine. The following images shows some epipolar lines and a few point pairs:

The rectified SURF keypoints look fine too, consider the following small sample for inspection, d is disparity and erro is the difference between the y coordinate (zero for a perfect mapping):
(306.28, 139.00) <-> (284.15, 138.48): d = -22.13, erro = -0.52
(259.84, 150.72) <-> (234.34, 150.51): d = -25.50, erro = -0.21
(423.93, 151.01) <-> (425.24, 150.71): d = 1.30, erro = -0.30
(220.98, 151.05) <-> (190.53, 151.05): d = -30.45, erro = -0.00
(354.21, 157.88) <-> (346.19, 157.91): d = -8.02, erro = 0.04
(304.17, 161.58) <-> (289.66, 161.80): d = -14.51, erro = 0.22
(229.47, 162.44) <-> (203.86, 162.27): d = -25.61, erro = -0.17
(406.54, 262.40) <-> (442.38, 262.91): d = 35.84, erro = 0.50
(361.67, 290.02) <-> (399.54, 289.98): d = 37.87, erro = -0.04
(356.44, 293.49) <-> (394.51, 292.96): d = 38.07, erro = -0.53
(340.01, 339.44) <-> (318.47, 339.75): d = -21.54, erro = 0.31
(245.47, 360.89) <-> (204.93, 360.18): d = -40.55, erro = -0.71
...
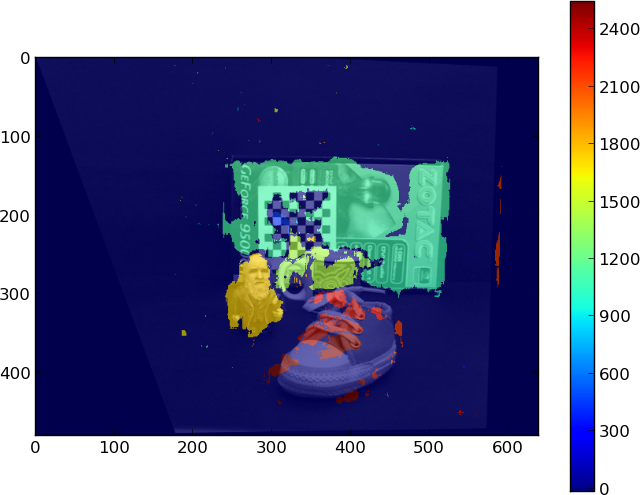
Now, the problem. The following image shows the two rectified images overlaped:

The ZOTAC word printed in the box is a good example. The word is in the same plane and, ideally, should present similar disparity. But the observed shearing will produce small disparities for "Z pixels" compared to disparities for "C pixels".
Actually, it's not an OpenCV issue. I implemented Hartley's algorithm from scratch using Python and NumPy and got the same results. What is the matter with Hartley's algorithm? Can StereoBM handle this problem? Or have I made some mistake?