Revision history [back]

Loop & Zhang present a solution in this paper. They use a shearing transform to reduce the distortion introduced by the projective transform that mapped the epipoles to infinity (ie, that made the epipolar lines parallel). Consider the shearing transform

     | k1 k2 0 |
S =  | 0   1 0 |.
     | 0   0 1 |

Let w and h be image width and height respectively. Consider the four midpoints of the image edges:

a = ((w-1)/2, 0, 1),
b = (w-1, (h-1)/2, 1),
c = ((w-1)/2, h-1, 1) and
d = (0, (h-1)/2, 1).

According to Loop & Zhang:

(...) we attempt to preserve perpendicularity and aspect ratio of the lines bd and ca

Let H be the rectification homography and let a' = Ha be a point in the affine plane by dividing through so that a'[2] = 1 (note a'[2] is the third component, ie, a' = (a'[0], a'[1], a'[2])). Let

x = b' - d',
y = c' - a'

According to Loop & Zhang:

As the difference of affine points, x and y are vectors in the euclidean image plane. Perpendicularity is preserved when (Sx)^T(Sy) = 0, and aspect ratio is preserved if [(Sx)^T(Sx)]/[(Sy)^T(Sy)] = w²/h².

The real solution presents a closed-form:

k1 = (h²x[1]² + w²y[1]²)/(hw(x[1]y[0] - x[0]y[1])) and
k2 = (h²x[0]x[1] + w²y[0]y[1])/(hw(x[0]y[1] - x[1]y[0]))

up to sign (the positive is preferred).

This is the result after applying shearing S on the left image:

Now the left and right images overlaped:

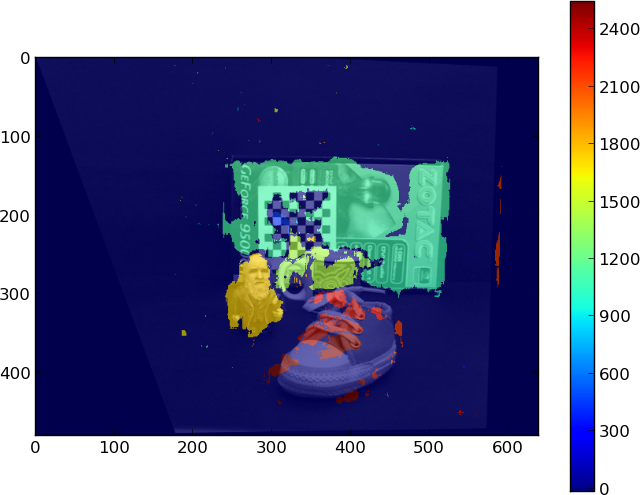
Finally, OpenCV stereo method StereoBM can compute a reasonable result for disparity: