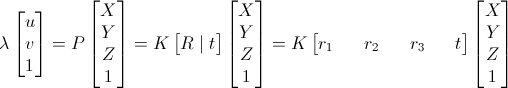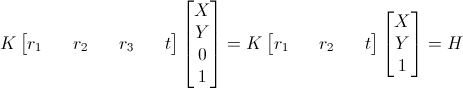Yes that is a correct assumption. To understand why, recall that a homography is an arbitrary linear mapping between two planes, in your case between a world plane and the image plane. The pinhole camera model specifies the projection of arbitrary 3d world points as
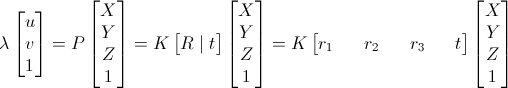
A homography requires that the world points lie on a plane, adding an additional constraint to the projection equation above. Because the absolute position of the camera and plane in world coordinates is not relevant for the projection, only their relative pose to each other (specified by R and t), we can arbitrarily require that the 3d world points lie on the X-Y world plane (Z=0) without any loss of generality. This simplifies the projection equation down to
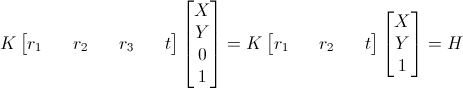
This is the trick used by Zhang as part of his flexible camera calibration technique (used by OpenCV) for example.