Retrieve yaw, pitch, roll from rvec
I need to retrieve the attitude angles of a camera (using cv2 on Python).
- Yaw being the general orientation of the camera when on an horizontal plane: toward north=0, toward east = 90°, south=180°, west=270°, etc.
- Pitch being the "nose" orientation of the camera: 0° = horitzontal, -90° = looking down vertically, +90° = looking up vertically, 45° = looking up at an angle of 45° from the horizon, etc.
- Roll being if the camera is tilted left or right when in your hands: +45° = tilted 45° in a clockwise rotation when you grab the camera, thus +90° (and -90°) would be the angle needed for a portrait picture for example, etc.
I have yet rvec and tvec from a solvepnp().
Then I have computed:
rmat = cv2.Rodrigues(rvec)[0]
If I'm right, camera position in the world coordinates system is given by:
position_camera = -np.matrix(rmat).T * np.matrix(tvec)
But how to retrieve corresponding attitude angles (yaw, pitch and roll as describe above) from the point of view of the observer (thus the camera)?
I have tried implementing this : http://planning.cs.uiuc.edu/node102.h... in a function :
def rotation_matrix_to_attitude_angles(R) :
import math
import numpy as np
cos_beta = math.sqrt(R[2,1] * R[2,1] + R[2,2] * R[2,2])
validity = cos_beta < 1e-6
if not validity:
alpha = math.atan2(R[1,0], R[0,0]) # yaw [z]
beta = math.atan2(-R[2,0], cos_beta) # pitch [y]
gamma = math.atan2(R[2,1], R[2,2]) # roll [x]
else:
alpha = math.atan2(R[1,0], R[0,0]) # yaw [z]
beta = math.atan2(-R[2,0], cos_beta) # pitch [y]
gamma = 0 # roll [x]
return np.array([alpha, beta, gamma])
but it gives me some results which are far away from reality on a true dataset (even when applying it to the inverse rotation matrix: rmat.T).
Am I doing something wrong?
And if yes, what?
All informations I've found are incomplete (never saying in which reference frame we are or whatever in a rigorous way).
Thanks.
Update:
Rotation order seems to be of greatest importance.
So; do you know to which of these matrix does the cv2.Rodrigues(rvec) result correspond?:
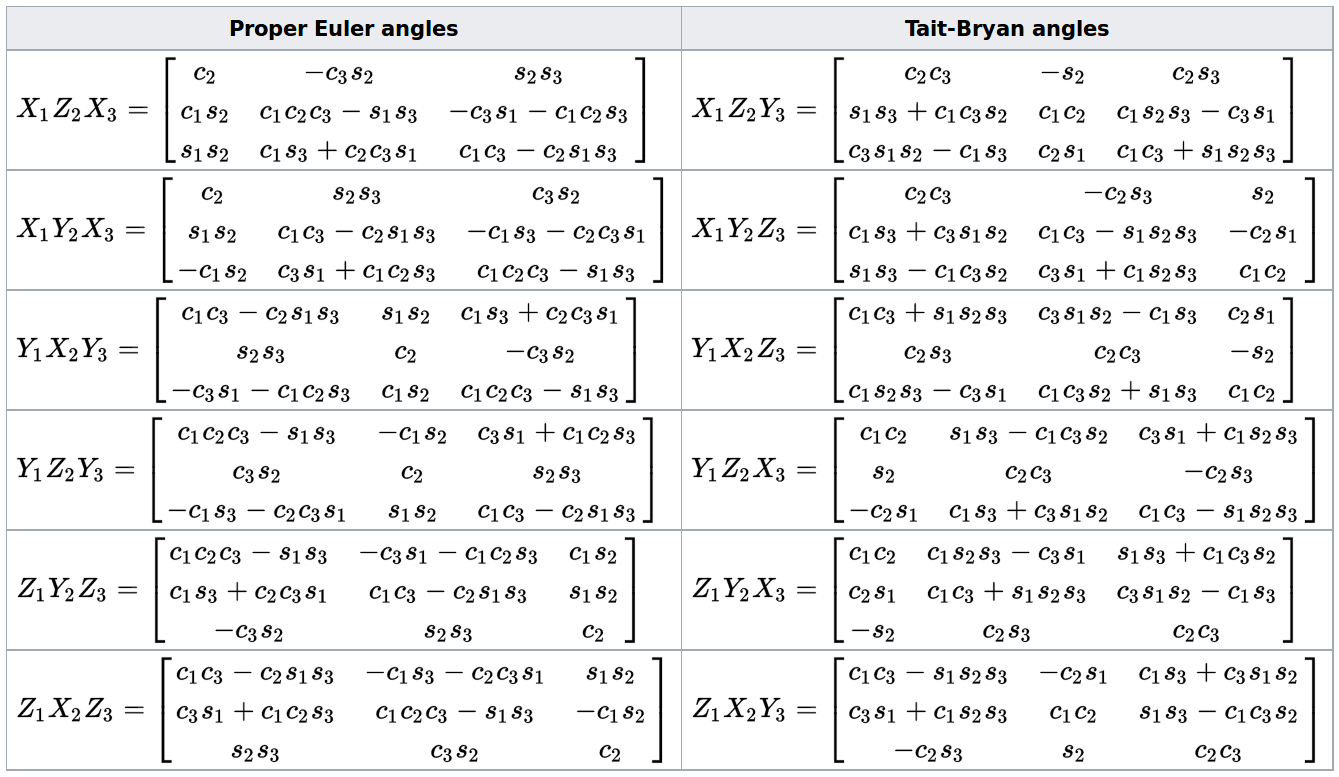
From: https://en.wikipedia.org/wiki/Euler_a...
Update:
I'm finally done. Here's the solution:
def yawpitchrolldecomposition(R):
import math
import numpy as np
sin_x = math.sqrt(R[2,0] * R[2,0] + R[2,1] * R[2,1])
validity = sin_x < 1e-6
if not singular:
z1 = math.atan2(R[2,0], R[2,1]) # around z1-axis
x = math.atan2(sin_x, R[2,2]) # around x-axis
z2 = math.atan2(R[0,2], -R[1,2]) # around z2-axis
else: # gimbal lock
z1 = 0 # around z1-axis
x = math.atan2(sin_x, R[2,2]) # around x-axis
z2 = 0 # around z2-axis
return np.array([[z1], [x], [z2]])
yawpitchroll_angles = -180*yawpitchrolldecomposition(rmat)/math.pi
yawpitchroll_angles[0,0] = (360-yawpitchroll_angles[0,0])%360 # change rotation sense if needed, comment this line otherwise
yawpitchroll_angles[1,0] = yawpitchroll_angles[1,0]+90
That's all folks!


One thing to note is that solvePnP returns the world coordinates relative to the camera, and you will need to invert the transformation if you need the orientation of the camera with respect to the world.
that's what I've already done, see the main post. And thanks to LBerger, I've already read that post many time; it's C++ related and it doesn't help a lot...
I wonder; what is the convention used by OpenCV to operate rotation ? In which order ? It's perhaps only a gap between how I imagine these 3 rotations and the reality. For me, with a normal frame, Z pointing upward, first rotation is around Z (yaw), then second rotation is around X axis (pitch) and finally the third one is around the new Z" (roll). But how are the standard camera axis oriented for OpenCV ? And the world reference frame ?
The rotation matrix is independent of operation and stores the complete rotational information. When decomposing it to euler angles you choose the order of those rotations.
The camera coordinates are x is right, y is down, z is out into the world. The world coordinates are defined by the points you use solvePnP with.
Ok, interesting. Thanks. So if I use a world coordinate system as follow: East=+X, North=+Y, and up=+Z, an horizontal camera looking toward east would yield these angles (in degrees): yaw=0, pitch=270 and roll=0. Am I right?
For the moment, it seems I have to add 90° to my roll angle (as found by my function in first post). I can't figure out why. I would have tell to add this value to the pitch angle as the Z camera axis is tilted 90° from the world Z axis.
And if I want to retrieve azimuth values, I must rotate the yaw values the other way, so: azimuth=360-yaw. This seems to work and I understand why.
Hmm, nope. A camera looking east would have a yaw component of magnitude 90. Positive or negative, I'm not sure without coloring my fingers, but I can tell it's needed.
My bad; you're right, I was tired. So east=-90° (positive rotation is always given clockwise while looking in the same direction as the axis perpendicular to the plane in which the rotation takes place). Anyway, I need to retrieve azimuth after, so by changing the rotation: azimuth = 360-yaw. This is clear to me.
So it's not the main point.
I would have expected 270 or -90 for the pitch angle for an horizontal camera, and in fact it's almost already near 0°.
And I would have expected a near 0° roll angle for an untilted camera, and there, it's -90° !
I do not understand why.
Nope, I just worked it out.
The yaw 90 puts the camera x = -y, camera y = x, camera z = z
Then Roll -90 then rotates around the camera x so you get camera x = -y, camera y = -z, camera z = x, which is what you want. If you did pitch -90, you would be rotating around the y, and would get camera x = -z.
Any yaw and a pitch of -90 gives you your camera x = down, which would mean your camera is turned so the right side of the image is down.
But by definition, roll is an intrinsic rotation around y and pitch around x.
I need to figure out the intrinsic rotation order for OpenCV.
I supposed it is: yaw, then pitch, an finally roll (for a "normal" frame, Z pointing up, x to the right and y to the front). Edit: No, I'm wrong with that assumption. Roll is effectively around x and pitch around y. I just figure it out.
Ah, no. By definition, pitch is y and roll is x. Always has been. Check the link in your answer.