Now in addition to the my previous thread regarding isotropic linear diffusion smoothing, I want to solve the non-linear version of it based on the Perona-Malik approach. Again we have the following formula:
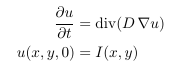 (1)
(1)
, where D is not a constant but varies across the image domain. A popular choice is the Perona-Malik diffusivity which can be given as:
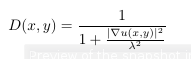 (2)
(2)
where λ is the contrast parameter. ∇u(x, y) is the gradient of the image at pixel (x, y). It seems that KAZE features embed this functionality, therefore I have a look at the source code. Specifically the formula (2) is implemented with the following function:
/* ************************************************************************* */
/**
* @brief This function computes the Perona and Malik conductivity coefficient g2
* g2 = 1 / (1 + dL^2 / k^2)
* @param Lx First order image derivative in X-direction (horizontal)
* @param Ly First order image derivative in Y-direction (vertical)
* @param dst Output image
* @param k Contrast factor parameter
*/
void pm_g2(const cv::Mat &Lx, const cv::Mat& Ly, cv::Mat& dst, float k) {
Size sz = Lx.size();
dst.create(sz, Lx.type());
float k2inv = 1.0f / (k * k);
for(int y = 0; y < sz.height; y++) {
const float *Lx_row = Lx.ptr<float>(y);
const float *Ly_row = Ly.ptr<float>(y);
float* dst_row = dst.ptr<float>(y);
for(int x = 0; x < sz.width; x++) {
dst_row[x] = 1.0f / (1.0f + ((Lx_row[x] * Lx_row[x] + Ly_row[x] * Ly_row[x]) * k2inv));
}
}
}
However, while I am trying to use it regarding to what @LBerger came up in the other thread I cannot get the correct output. What do I miss again?


