isotropic non-linear diffusion smoothing (Perona-Malik)
Now in addition to the my previous thread regarding isotropic linear diffusion smoothing, I want to solve the non-linear version of it based on the Perona-Malik approach. Again we have the following formula:
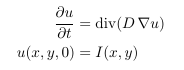 (1)
(1)
, where D is not a constant but varies across the image domain. A popular choice is the Perona-Malik diffusivity which can be given as:
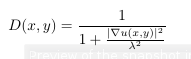 (2)
(2)
where λ is the contrast parameter. ∇u(x, y) is the gradient of the image at pixel (x, y). It seems that KAZE features embed this functionality, therefore I have a look at the source code. Specifically the formula (2) is implemented with the following function:
/* ************************************************************************* */
/**
* @brief This function computes the Perona and Malik conductivity coefficient g2
* g2 = 1 / (1 + dL^2 / k^2)
* @Param Lx First order image derivative in X-direction (horizontal)
* @Param Ly First order image derivative in Y-direction (vertical)
* @Param dst Output image
* @Param k Contrast factor parameter
*/
void pm_g2(const cv::Mat &Lx, const cv::Mat& Ly, cv::Mat& dst, float k) {
Size sz = Lx.size();
dst.create(sz, Lx.type());
float k2inv = 1.0f / (k * k);
for(int y = 0; y < sz.height; y++) {
const float *Lx_row = Lx.ptr<float>(y);
const float *Ly_row = Ly.ptr<float>(y);
float* dst_row = dst.ptr<float>(y);
for(int x = 0; x < sz.width; x++) {
dst_row[x] = 1.0f / (1.0f + ((Lx_row[x] * Lx_row[x] + Ly_row[x] * Ly_row[x]) * k2inv));
}
}
}
However, while I am trying to use it regarding to what @LBerger came up in the other thread I cannot get the correct output. What do I miss again?
I see that the author apply some scalar non-linear diffusion step functionality which I do not really understand what it is about it, here is the function. I tried what @Guanta suggested in the other thread
I think in the evolution_ - Vector (KAZEFeatures.h) are the evolutions over time, so if you'd take the last element and then from that element's struct (TEvolution.h) the Lsmooth Mat should be the image which has been smoothed. To create the evolution_-vector you need to call
Create_Nonlinear_Scale_Space().
but it did not give a good output :-(.


So I haven't studied link given. I have read perona malik paper
I proposed this program
@LBerger man I really appreciate your time to help me. I tested you code and it seems to provide the expected result :-). However, if it is not a harsh I would like you to provide some comments in your code in order to understand what you are doing in each step, I guess this would be helpful for other users as well. Moreover, again make it an answer in order to accept it as correct. Again many thanks ;-)
That's an interesting question and I like giving my time for tah's sort of problem
I don't think that code is ready for an answer. In this paper equation 8 (p 632) it's OK but equation (9) and (10) I m' not sure. I have inserted some comment in code
I think my code is good because i have found this post ( sorry it's in french)
super!!! thanks again ;-)