Revision history [back]

Stitching pictures from rotating camera

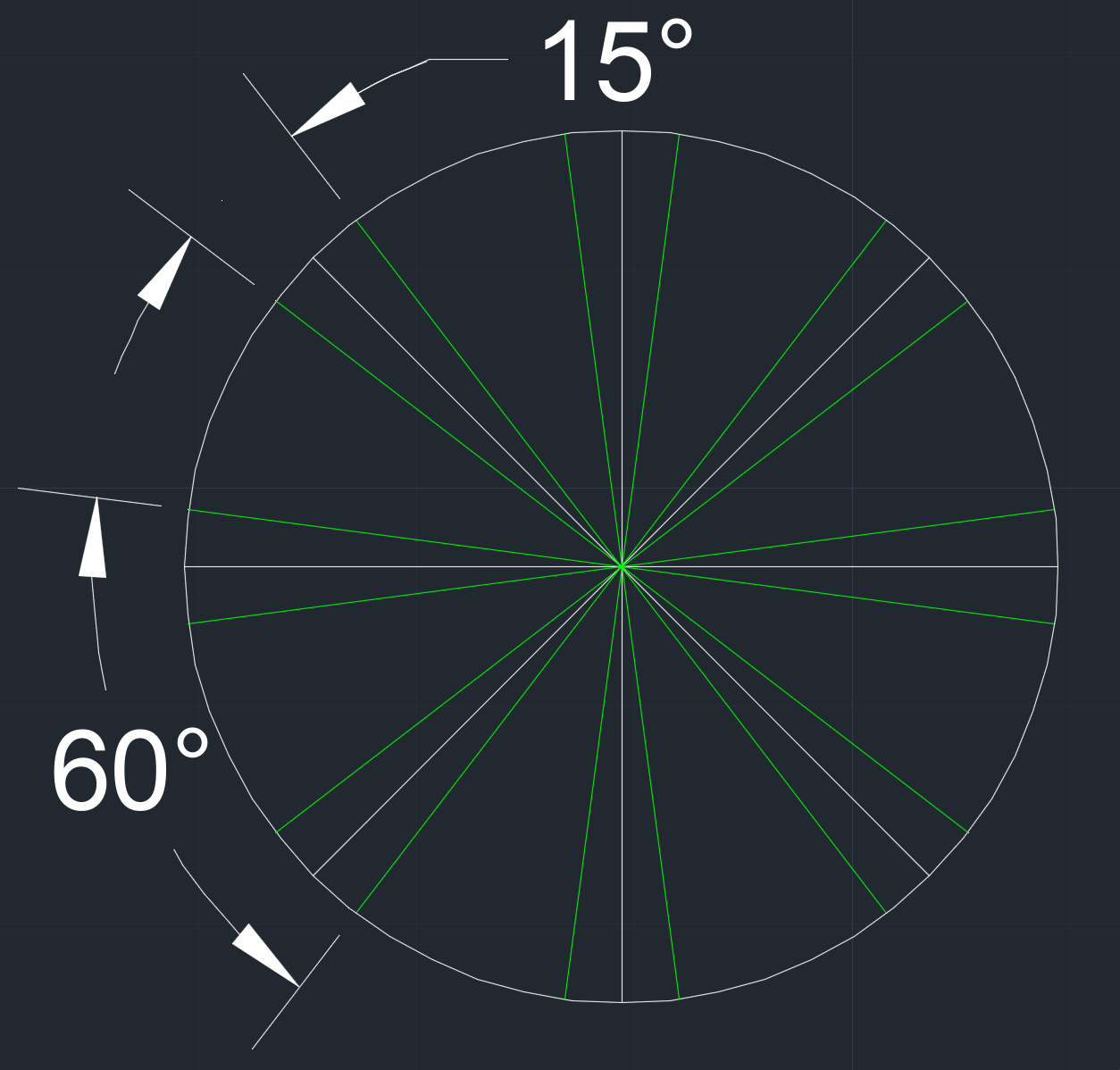
I have a security camera that is rotating at 1rpm. It is set to 60° FOV, and configured on a preset to take 8 pictures in 1 rotation. With the knowledge of the FOV as well as the picture's direction (angle), how could I use OpenCV to stitch the 8 pictures together into a single 360° panoramic?

With 60° FOV at 8 pictures per rotation, there are 15° of overlap on each side of the picture.

With this information, it possible for me to compute the homography matrix manually? If so, I would greatly appreciate some direction!

image description

Stitching pictures from rotating camera

With 60° FOV at 8 pictures per rotation, there are 15° of overlap on each side of the picture.

With this information, it possible for me to compute the homography matrix manually? If so, I would greatly appreciate some direction!

image description

Update:

Thank you @Eduardo for pointing me to this tutorial of stitching for a rotating camera. Following the tutorial, I am trying to compose the c1Mo and c2Mo matrices representing the "poses" of the camera, whereby the difference in the "poses" is the camera's rotation. Using Blender, I have modeled the scene, which involves the camera (with its known intrinsics inputted into Blender) in 2 "poses":

Origin pose, looking down the Z axis.
-22.5° rotation around the Y axis.

image description

Using this script to get the P matrices of the two "poses" (which I assume are supposed to be the c1Mo and c2Mo in the tutorial), the tutorial code produces a H matrix. However, the visual output is the following:

image description

Am I missing some key piece in this solution? Making changes to c1Mo and c2Mo, based on rotation around different axes, or even random changes, (or even the K matrix) lead to the same visual results.