Stitching pictures from rotating camera

asked 2020-10-02 05:57:32 -0600

seva gravatar image

updated 2020-10-04 00:00:49 -0600

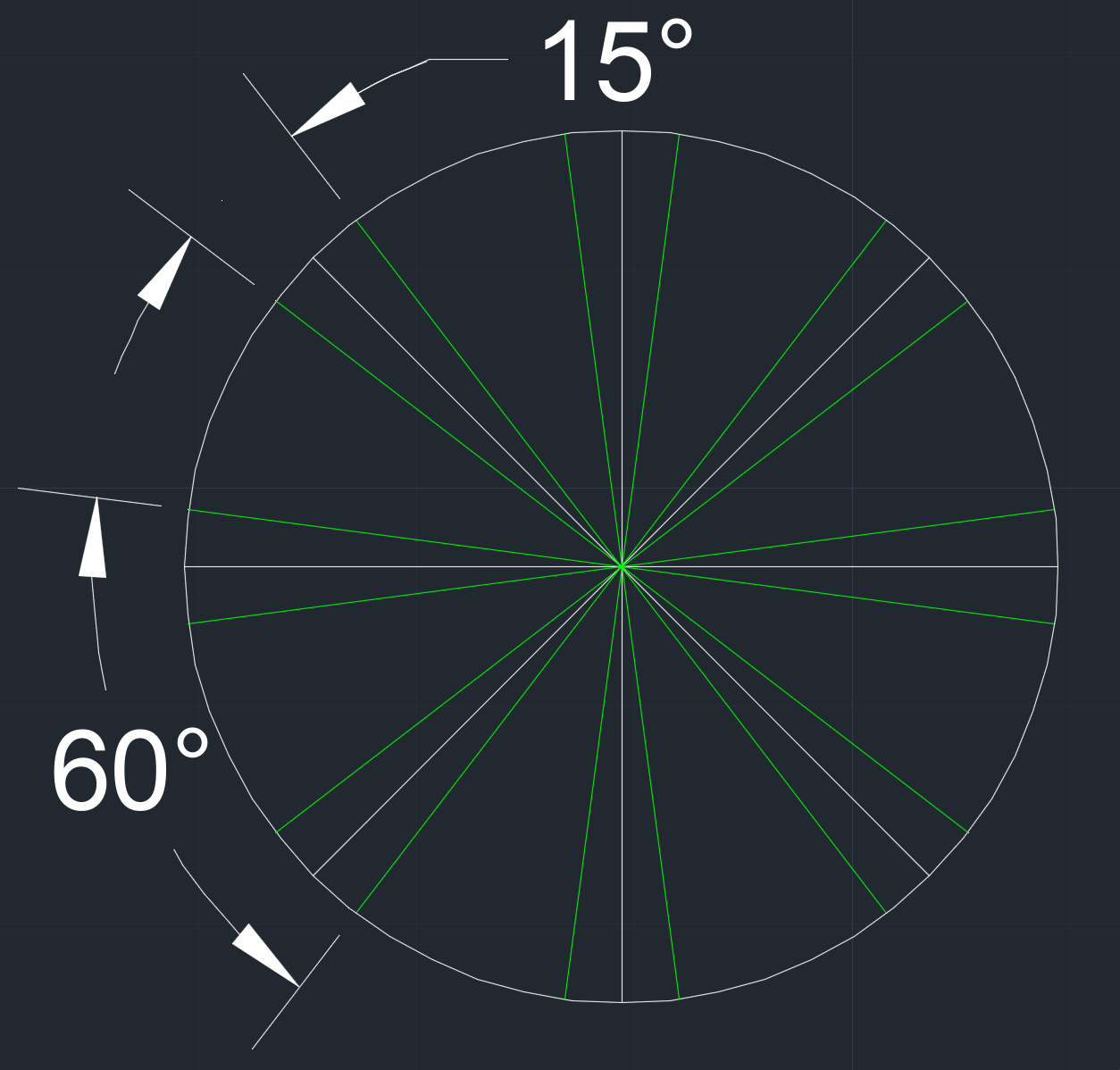
I have a security camera that is rotating at 1rpm. It is set to 60° FOV, and configured on a preset to take 8 pictures in 1 rotation. With the knowledge of the FOV as well as the picture's direction (angle), how could I use OpenCV to stitch the 8 pictures together into a single 360° panoramic?

With 60° FOV at 8 pictures per rotation, there are 15° of overlap on each side of the picture.

With this information, it possible for me to compute the homography matrix manually? If so, I would greatly appreciate some direction!

image description

Update:

Thank you @Eduardo for pointing me to this tutorial of stitching for a rotating camera. Following the tutorial, I am trying to compose the c1Mo and c2Mo matrices representing the "poses" of the camera, whereby the difference in the "poses" is the camera's rotation. Using Blender, I have modeled the scene, which involves the camera (with its known intrinsics inputted into Blender) in 2 "poses":

  1. Origin pose, looking down the Z axis.
  2. -22.5° rotation around the Y axis.

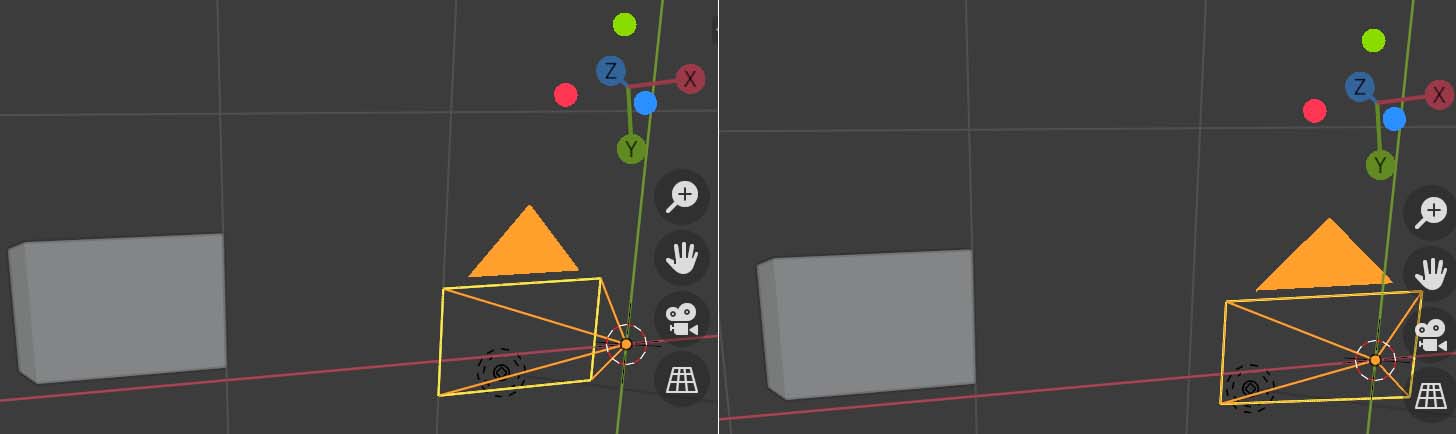
image description

Using this script to get the P matrices of the two "poses" (which I assume are supposed to be the c1Mo and c2Mo in the tutorial), the tutorial code produces a H matrix. However, the visual output is the following:

image description

Am I missing some key piece in this solution? Making changes to c1Mo and c2Mo, based on rotation around different axes, or even random changes, (or even the K matrix) lead to the same visual results.

edit retag flag offensive close merge delete

Comments

This can be a good start.

Eduardo gravatar imageEduardo ( 2020-10-02 07:07:59 -0600 )edit

Thank you the reference, @Eduardo. I followed the guide, and have tried to apply it to two pictures that have been taken with the security camera. The pictures were taken with the camera at 0° and 22.5° rotation. I know the camera intrinsic matrix, but am stuck trying to figure out c1Mo and c2Mo. Are these homographic projection matrices? Is their difference is supposed to equate to the 22.5° rotation in the Y axis?

seva gravatar imageseva ( 2020-10-03 08:51:18 -0600 )edit

What is important is that for a rotating camera, the Homography is H = K x R x K^-1. With K the camera intrinsic parameters and R the rotation matrix between the two camera viewpoints. Have a look at this page to have an overview of the camera model.

Eduardo gravatar imageEduardo ( 2020-10-03 12:33:51 -0600 )edit

Again, thank you for your help @Eduardo. I have studied the camera model in depth, and see the H = K x R x K^-1 in the tutorial code. I have updated the original question with my results, and would definitely appreciate your further guidance. Also, I am using both the code in the tutorial, as well as this code when running my tests.

seva gravatar imageseva ( 2020-10-04 00:05:18 -0600 )edit

You can try this code

LBerger gravatar imageLBerger ( 2020-10-04 03:06:29 -0600 )edit

Computing R from c1Mo and c2Mo is just an easy way to compute the rotation between the two camera viewpoints in Blender.

In your case, you don't know c1Mo and c2Mo unless you are using a calibration board, or explicitly computing it.

For R, you should be able compute it using the angle. Look at 3d rotation matrix, and be careful about the camera coordinates system.

Eduardo gravatar imageEduardo ( 2020-10-05 05:14:17 -0600 )edit
add a comment