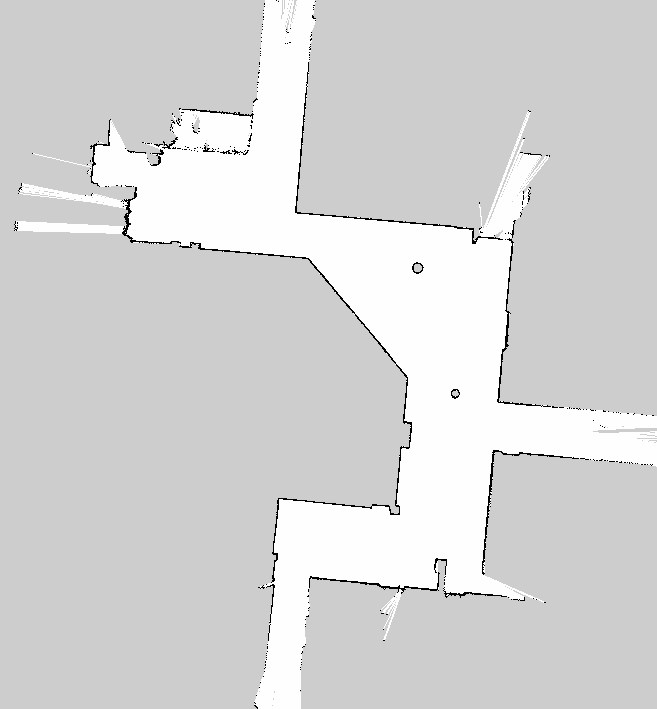
I can't upload my image or publish links so I'll describe my map. It is a robotics map that is similar to the one you will find if you Google "Centibots: the Hundred-Robots Project". Take away the coloured lines from that image and that is a good representation of what I am working with.
Essentially, I am trying to orient the image so that the longest walls are aligned horizontally to within a hundredth of a degree. This also includes hallways that have bumpy walls and possibly insets. It's fairly easy to do in GIMP, but automating it has turned out to be a rabbit hole.
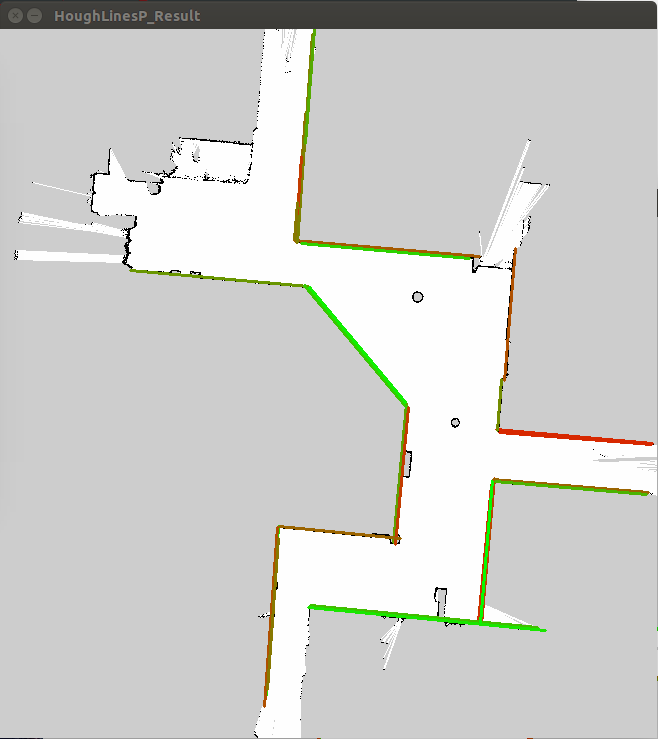
The first thing I did was look into using Houghlines for this, but it doesn't help me find the "best" lines in my image. It just produces a set of lines and angles; this is a problem because there may be a lot of lines in my map and I need to know the length and angle of each of them to evaluate the best map orientation. After a lot of tinkering I wasn't able to get the function to properly detect precise location of my lines, even after giving rho and theta a precision of 0.01 and np.pi/18000 respectively.
Ok, that's fine, so I decided I would take a different approach. I would use findNonZero to get the location of all black pixels (in a bw image). Apply a rotation transform of 0 to 180 degrees and then count the number of black pixels that share the same Y coordinate (within a small tolerance).
This is my code for doing that and it is extremely processor intensive. So much so that It will take 10 minutes to compute the result of 6100 points. Even further down the rabbit hole I went to try and use multi-core processing in Python and shared memory access. This is what I have right now but I think there is a better way. I will provide examples of my actual maps once I reach the points required.
import cv2
import numpy as np # used for matrix calculations with opencv
class align_map():
def __init__(self, map_name):
# Set precision
STEP_ANGLE = 0.01 # degrees
MAX_ANGLE = 1
image = cv2.imread(map_name)
width, height = cv2.imread(map_name, 0).shape[:2]
bw_image = cv2.bitwise_not(image)
self.black_pixel_coords = cv2.findNonZero(bw_image)
# Find bounding box
x,y,w,h = cv2.boundingRect(self.black_pixel_coords)
diagonal = np.ceil(np.sqrt(w*w + h*h))
self.diagonal_center = np.ceil(diagonal/2)
# Determine size of result matrix
result_mat_cols = np.ceil(diagonal)
accum_angle = 0
result_mat_rows = MAX_ANGLE / STEP_ANGLE
self.result_mat = np.zeros((result_mat_rows + 1, result_mat_cols), np.uint32)
self.job_pool = []
# Recenter all y_coords at diagonal midpoint
center_x = x + w/2;
center_y = y + h/2;
y_offset = self.diagonal_center - center_y
x_offset = self.diagonal_center - center_x
for row in self.black_pixel_coords:
row[0][0] = row[0][0] + x_offset
row[0][1] = row[0][1] + y_offset
new_list = list()
index = 0
while (accum_angle < MAX_ANGLE):
rotation_affine = cv2.getRotationMatrix2D((self.diagonal_center, self.diagonal_center), accum_angle, 1)
test = cv2.transform(self.black_pixel_coords.astype('double'), rotation_affine)
rounded = np.round(test).astype('int')
for row in rounded:
col_index = int(row[0][1])
self.result_mat[index, col_index] = self.result_mat[index, col_index] + 1
Is there a better way to compute how to orient my map?