isotropic linear diffusion smoothing
I want to apply the denoising filter I named in the title which is based on the following equations:
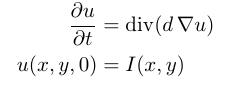
where d is a scalar constant diffusivity parameter, I(x, y) is the initial noisy image, and u(x, y, t)
is the image obtained after a diffusion time t lets say 5, 10 and 30. However, I am quite confused about which function to use and how, in order to achieve this in OpenCV. I have the feeling that it is quite simple but for some reason I am confused. Does anyone have an idea?
Here is a sample image:

UPDATE
this is the result images after following @LBerger 's code, they are in time t = 0/t = 4 and d = 1:


, is it expected to be like that?
I think that something is wrong, because I am trying also to compare it with the gaussian smoothing. And according to the following formula:
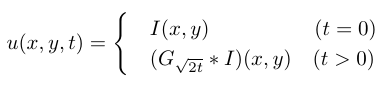
where G√2t (x, y) is the Gaussian kernel. This proves that performing isotropic linear diffusion for a time t with d = 1 is exactly equivalent to performing Gaussian smoothing with a σ = √(2t)
and applying the gaussian filter with the following code:
void gaussian_2D_convolution(const cv::Mat& src, cv::Mat& dst, const float sigma, const int ksize_x = 0, const int ksize_y = 0)
{
int ksize_x_ = ksize_x, ksize_y_ = ksize_y;
// Compute an appropriate kernel size according to the specified sigma
if (sigma > ksize_x || sigma > ksize_y || ksize_x == 0 || ksize_y == 0)
{
ksize_x_ = (int)ceil(2.0f*(1.0f + (sigma - 0.8f) / (0.3f)));
ksize_y_ = ksize_x_;
}
// The kernel size must be and odd number
if ((ksize_x_ % 2) == 0)
{
ksize_x_ += 1;
}
if ((ksize_y_ % 2) == 0)
{
ksize_y_ += 1;
}
// Perform the Gaussian Smoothing
GaussianBlur(src, dst, Size(ksize_x_, ksize_y_), sigma, sigma, BORDER_DEFAULT);
// show result
std::ostringstream out;
out << std::setprecision(1) << std::fixed << sigma;
String title = "sigma: " + out.str();
imshow(title, dst);
imwrite("gaussian/" + title + ".png", dst);
waitKey(260);
}
and calling it with gaussian_2D_convolution(img, smoothed, sqrt(2*5)); the two results of gaussian smoothing and isotropic linear smoothing in time t = 5 are respectively:


which are for sure not similar :-(.



Something like this :
@LBerger thanks for the response ;-), would be able though to provide some comments on the code.
Vectorial computation is very far but I remember well your equation is
du/dt=k.Laplacian(u)
You can use finite difference equation and it becomes :
u(t+1)-u(t) = k' laplacian(u(t)) and hence u(t+1) =u(t) + k' Laplacian(u(t))
k' is k by time unit. As you are not doing a real simulation of diffusivity you don't care.
Of course that's a brute force method I think you have read paper on subject. If you want to write something you can have a look here p 847
@LBerger thank you again for your help, running though your code I getting the result images that I have added in the update part of my initial question. They seem much more noisy than the original image, is that expected?
Yes with your first example it's working. Is it? But noisiy image is not very far from answer. But in this example if you use t=50 instead of 50 it's wrong. My algorithm is not good because it does not converge. Criteria given page 847 is not respected at all
I do not think that the it works even in the first example. Moreover, I do not think that the image should be noisy as it appears, rather than smoother like the result from the gaussian filter.
I don't understand your last comment. I have changed my program. Now I'm using diffusitvity coefficient time dependant. You can download here.
If you run program you can see that initial parameter are important (dt and diffusivity). I don't know method to reduce noise without this choice ( frequency, size of window...)
Again program given is not a reference I hope it's only a test to understand diffusion equation in image processing.
A way to improve this program is to consider D as function (x,y). Then laplacian is replace by your orignal expression and filter will become an adaptive filter (i have read some paper about this)
Just as a side note: If you are interested also in non-linear diffusion you can have a look at the KAZE-detector / desciptor, it is based on a non-linear diffusion scale-space if I remember correctly.
@Guanta thanks for the hint, that's actually my next step after I manage to accomplish this task :-). @LBerger thanks again for your hints and your help. Actually, I have opened a thread in the stackoverflow and there with the help of the user Miki who suggested me a solution based on your approach I managed to get somehow a good result.
However using the following code:
I cannot get the same result with the gaussian smoothing. An diffusion time of 5 corresponds to a
σ = √(2t) = 3.2for the gaussian