Rotate Landmarks

asked 2015-07-22 15:14:21 -0600

chr0x
201 ●1 ●2 ●10

updated 2015-07-23 06:39:48 -0600

Hello. I have various files with 2D coordinates describing faces of people. In OpenCV I'm using the circle function to draw each of these coordinates in a black background (Mat::zeros), so:

image description

In the program, the points are in a 2 x 70 matrix, where 70 is the number of landmarks used. The first row stores the X's, and second row stores the Y's

I have the centroid of each eye and, as can be seen in the image, a line linking these centroids. My objective is turn the angle of this line to 0 (in the example image it is ~ 1.9 degrees) and rotate the rest of the shape using the same rotation applied on the line, i.e. for this case for example, rotate all the shape -1.9, I guess.

I was using warpAffine to do the rotation, but it apply the operation in the image (object Mat), not in the coordinates and when I tried to use my Mat with the coordinates (the 2x70 matrix) it didn't worked. My question is: any way to perform the rotation (and then, scaling and translating) in the points, not in the image?

edit retag flag offensive close merge delete

Comments

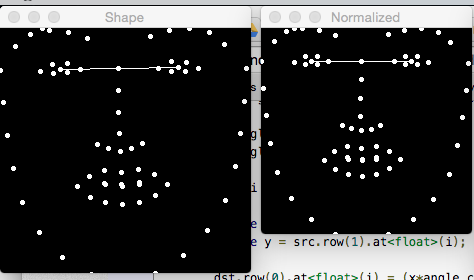
I've not seen a function that rotates a point, but you could easily write it yourself. cv::gemm does the multiplication, so you'd have to create a homogeneous vector for each point (x,y,1), and multiply it with your affine matrix (e.g. from getRotationMatrix2D).

FooBar ( 2015-07-23 02:07:58 -0600 )edit

Hi @FooBar , the idea of make the direct multiplication was the first thing I thought, actually I already confirmed (calculating manually) that it solves the problem if I simply multiply my 2x70 matrix by [cos angle sin angle; sin angle, cos angle] (where ";" means row division). Could you provide some code example for that? I didn't have much luck implementing it until now.

chr0x ( 2015-07-23 08:48:47 -0600 )edit

add a comment

3 answers

Sort by » oldest newest most voted

answered 2015-07-27 11:37:15 -0600

chr0x
201 ●1 ●2 ●10

updated 2015-07-31 23:03:32 -0600

Hi guys. As I promised on my last comment, here is the solution that I found (as I said, I don't think that is a elegant solution, but it works):

 Mat rotate_landmarks(Mat &src) {
    Mat dst = src.clone();

    Point2f l = get_left_eye_centroid(src);
    Point2f r = get_right_eye_centroid(src);

    Point2f center(
                   (r.x + l.x) / 2,
                   (r.y + l.y) / 2
                   );

    Mat rot = getRotationMatrix2D(center, get_alignment_angle(src), 1);

    double angle_cos = rot.at<double>(0,0);
    double angle_sin = rot.at<double>(1,0);

    for (int i = 0; i <= 66; i++) {

        double x = src.row(0).at<float>(i);
        double y = src.row(1).at<float>(i);

        dst.row(0).at<float>(i) = (x*angle_cos) - (y*angle_sin);
        dst.row(1).at<float>(i) = (y*angle_cos) + (x*angle_sin);

    }

    return dst;
}

I'm applying the rotation for each point, using:

        dst.row(0).at<float>(i) = (x*angle_cos) - (y*angle_sin);
        dst.row(1).at<float>(i) = (y*angle_cos) + (x*angle_sin);

I actually don't like this solution very much because I'm generating the rotationMatrix2D but it is not being used directly, that's because i'm not working with a conventional image matrix.

If someone have any solution that uses the rotationMatrix directly please add the answer to this topic and I probably will mark it as the best answer.

Thank to everyone that helped.

image description

edit flag offensive delete link

add a comment

answered 2015-07-28 01:19:17 -0600

albertofernandez
3259 ●6 ●39 ●56 https://es.linkedin.co...

What about this solution?

/** rotate points based on rot_mat */
void get_rotated_points(const std::vector<cv::Point2d> &points, std::vector<cv::Point2d> &dst_points, const cv::Mat &rot_mat){

for (int i = 0; i<points.size(); i++){
    Mat point_original(3, 1, CV_64FC1);
    point_original.at<double>(0, 0) = points[i].x;
    point_original.at<double>(1, 0) = points[i].y;
    point_original.at<double>(2, 0) = 1;

    Mat result(2, 1, CV_64FC1);

    gemm(rot_mat, point_original, 1.0, cv::Mat(), 0.0, result);

    Point point_result(cvRound(result.at<double>(0, 0)), cvRound(result.at<double>(1, 0)));

    dst_points.push_back(point_result);
 }
}


//rotate landmarks
get_rotated_points(landmarks, dst_landmarks, rot_mat);

edit flag offensive delete link

add a comment

answered 2015-07-23 03:49:36 -0600

StevenPuttemans

20029 ●16 ●82 ●207 http://stevenputtemans...

updated 2015-07-23 04:23:02 -0600

That is quite straightforward if you have the outer points of your line, you can do it this way:

double angle = atan( (point1.y – point2.y) / (point1.x – point2.x) );
Point2f pt(face_region.cols/2, face_region.rows/2);
Mat rotation = getRotationMatrix2D(pt, angle, 1.0);
Mat rotated_face;
warpAffine(face_region, rotated_face, rotation, Size(face_region.cols, face_region.rows));

Let me update with something I found on SO, right here.

If M is the rotation matrix you get from cv::getRotationMatrix2D, to rotate a cv::Point p with this matrix you can do this:

cv::Point result;
result.x = M.at<double>(0,0)*p.x + M.at<double>(0,1)*p.y + M.at<double>(0,2);
result.y = M.at<double>(1,0)*p.x + M.at<double>(1,1)*p.y + M.at<double>(1,2);

If you want to rotate a point back, generate the inverse matrix of M or use cv::getRotationMatrix2D(center, -rotateAngle, scale) to generate a matrix for reverse rotation.

--> for me that means that you can just replace M with the rotation matrix that we grabbed and then put in the original location of the points! Good luck!

edit flag offensive delete link

Comments

I think he does not have a problem rotating the whole image but retrieving afterwards the new coordinates of the landmarks. Elegant solution will be the one @FooBar suggested above, applying the transformation matrix to each homogenous vector. A less elegant solution could be to represent the landmarks as 1 pixel white points, rotate the whole image as you say, and then find the new coordinates by going through the image matrix and finding those white pixels x's and y's.

LorenaGdL ( 2015-07-23 04:17:10 -0600 )edit

@StevenPuttemans: regarding your update, that's exactly what we were talking about, multiplying transformation matrix by homogeneous vectors. However that solution you found it's quite inefficient, it can be solved with simple matrix by matrix multiplication without the need to access each element of M. Anyway, to the OP, just point out that with this approach he'll need to take care of the non-integer rotated coordinates he'll got.

LorenaGdL ( 2015-07-23 04:36:46 -0600 )edit

Guys, this approach didn't worked to me. I found another way, basically I get the angle between the two points:

atan(get_eyes_y_dis(shape)/get_eyes_x_dis(shape)) *180/CV_PI

shape is my 2x70 matrix and get_eyes... is the difference between the 2 eyes.

And then I build a new 2x70 matrix:

    for (int i = 0; i <= 70; i++) {       
        double x = shape.row(0).at<float>(i);
        double y = shape.row(1).at<float>(i);

        dst.row(0).at<float>(i) = (x*cos(angle)) - (y*sin(angle));
        dst.row(1).at<float>(i) = (y*cos(angle)) + (x*sin(angle));
}

DST is the new matrix...

It is rotating the matrix, but using the angle found ˜ -0.9 the only thing I did was increase the angle (the new angle between centroids is -56.306). Any idea where I'm w

chr0x ( 2015-07-23 12:03:20 -0600 )edit

Hi guys. I just found a solution, it's not very elegant, and I probably gonna refactor this soon, but it works!. The problem was I was using the "image's center" as the 'center' variable to generate the rotation matrix, the correct way to do this is not using the image center but the center between the eyes distance (I tried to post the solution here as a answer but I can't because I registered here in the site recently, I will try to repost after 2 days with the code).

chr0x ( 2015-07-23 15:06:18 -0600 )edit

Strange that my code does not work, I have a working test setup here ... which does exactly the rotation. Indeed against image center, but that seems best to me, you want to loose as less image information as possible due to your reprojection.

StevenPuttemans ( 2015-07-24 01:56:56 -0600 )edit

@StevenPuttermans , I think that it didn't work to me more because of my setup, not because of any problem in your code. For example, this way to find the center will not work for me:

Point2f pt(face_region.cols/2, face_region.rows/2);

That's because I'm using a 2x70 matrix, not a regular image matrix (I don't know if it is a good approach, but it works). I have a draw_shape function that generates the image and it can return in different scales so I tried to work with this image to get the center and I found that problem related to using the image center (as I described in last comment). I will try to post the code I used (I need more 2 days in answers.opencv to be able to answer my own question).

Your answer helped me a lot anyway, thanks.

chr0x ( 2015-07-24 06:08:52 -0600 )edit

add a comment

Rotate Landmarks

Comments

3 answers

Comments

Links

Question Tools

Stats

Related questions

Rotate Landmarks edit

Comments

3 answers

Comments

Links

Question Tools

Stats

Related questions

Rotate Landmarks