Find the high frequency part of the 1D haar wavelet transform

edit

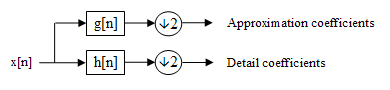
This post will hopefully answer 1), but not 2), since I'm not familiar with that formulation.

The 1D Haar transform is incredibly simple to code (yet I always see complex explanation). Here is one way to do it:

// Unormalized version
// assumes width is a power of 2
void Haar1D(float *A, int width)
{
    float tmp[width]; // some compilers might not like this

    while(width > 1) {
        width /= 2;

        for(int i=0; i < width; i++) {
            tmp[i] = (A[2*i] + A[2*i+1]) * 0.5;
            tmp[width + i] = (A[2*i] - A[2*i+1]) * 0.5;
        }

        memcpy(A, tmp, width*2*sizeof(float));
    }
}

The value at A[0] is the average of the 1D array, every other value are the detail coefficients. They are the "edge" information at different resolutions, so they might be the high frequency values you are interested in.

The normalized version is similar to the above

void Haar1D(float *A, int width)
{
    float norm = 1.0f/sqrt(width);

    for(int i=0; i < width; i++)
        A[i] *= norm;    

    float tmp[width];

    while(width > 1) {
        width /= 2;

        for(int i=0; i < width; i++) {
            tmp[i] = (A[2*i] + A[2*i+1]) * sqrt(2);
            tmp[width + i] = (A[2*i] - A[2*i+1]) * sqrt(2);
        }

        memcpy(A, tmp, width*2*sizeof(float));
    }
}

I've used these functions in the past based on material from http://www.multires.caltech.edu/teaching/courses/waveletcourse/