Finding depth of an object using 2 cameras

edit

Hi, I am new to stereo imaging and learning to find depth of an object.

I have 2 cameras kept separately looking at a cardboard surface.

Given :

• 8 points marked on the cardboard surface.
• Captured one image each from both the camera.
• Identified (x,y) coordinates of all 8 points in both the images.

Problem : Find the depth of each point i.e. distance of each point from the cameras.

I tried solving it using following approach but I got weird result :

1. Noted down 8 common points from both the left and right images captured from 2 different cameras.
2. Determined Fundamental Matrix between both the images using 8 points.
3. The fundamental matrix F relates the points on the image plane of one camera in image coordinates (pixels) to the points on the image plane of the other camera in image coordinates
   • Opencv Function : cv::findFundamentalMat()
   • Input to the function : 8 common points from both the image
   • Output = Fundamental matrix of 3x3
4. Performed stereo rectification
   • It reprojects the image planes of our two cameras so that they reside in the exact same plane, with image rows perfectly aligned into a frontal parallel configuration.
   • Opencv Function : cv::stereoRectifyUncalibrated()
   • Input to the function : 8 common Points from the images and fundamental matrix
   • Output = Rectification matrices H1 and H2 for both the images.

5. Determined depth of a point

   • Trying to find the depth of a point which is aprox. 39 feet (468 inches) away from the camera.
   • Formula to find depth is Z = (f * T) / (xl – xr)
   • Z is depth, f is focal lenth, T is distance between camera, xl and xr are x coordinate of a point on left image and right image respectively.

   • Following are the values taken for the variables :

     • f = From the determined camera intrinsic of the camera, I got fx and fy. So I found out f = sqrt(fxfx + fyfy)
     • T = 2 cameras are kept apart 36 feet i.e. 432 inches. So, I gave T = 432
     • xl and xr are x values of the point from left and right images which are perspective transformed using rectification matrices H1 and H2.

   • But I got very weird result. You can look at the screenshot of my experimentation and result.

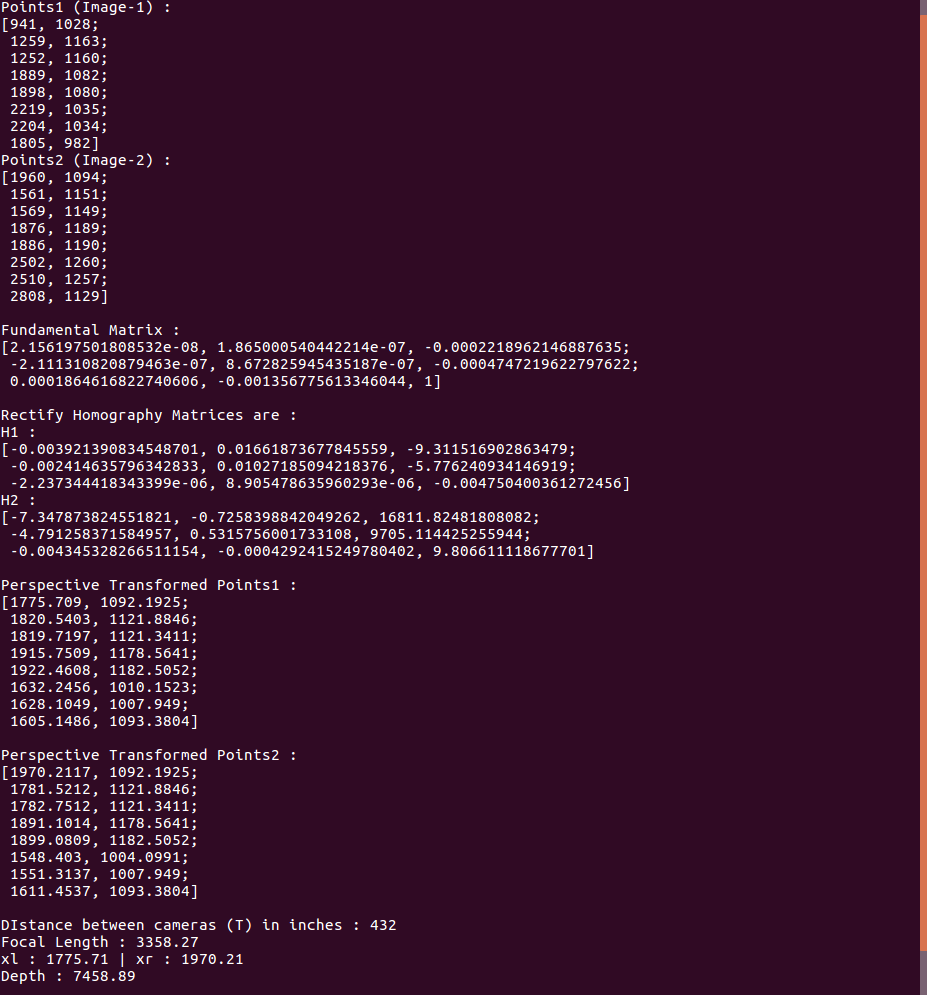
So could someone tell me the approach I am taking is right or wrong ?