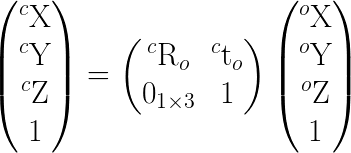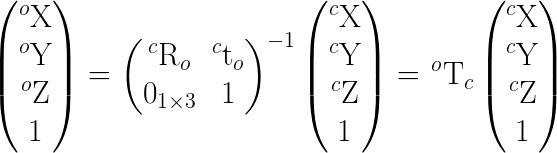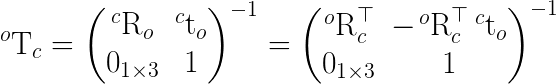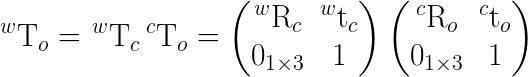Transformation of 3d points and camera poses to a new world frame
This post might be long but I am providing full code to replicate what I am seeing in hope of receiving help. In short, all I am trying to do is use 4x4 homogeneous matrices to transform current data to a new world frame. This should be as easy as multiplying 4x4 matrices with other 4x4 (homogeneous matrix of rotation, center of camera) or 4x1 (homogeneous points).
- Pt' = T * Pt, where Pt is made homogeneous
- C1' = T * C1 where C1 = [R | C] homogeneous
However the rotation results for C1' are not correct as I show below. Assuming I have a matrix T that transforms points from W to W', should not T also transform C1 to C1' ? Cameras are just another reference frame. That is how transformation matrices are combined I thought. So I am probably not understanding or missing something.
So the questions is: How to transform, using a 4x4 homogeneous transformation matrix, a set of
- 3D points
- Camera poses (Rotation, centers)
to a new world frame.
I went through the exercise to try figure what is going on using generated data.
- Generate some data
- Transform it and calculate the new camera poses
- Try to figure out how to transform the initial data to the new world frame
So here is the generation of the data at the initial World frame, nothing special...
cv::Matx33d cameraMatrix(1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
0.0, 0.0, 1.0);
cv::Mat distCoeffs;
// 3D points.
std::vector<cv::Point3d> points3d;
points3d.push_back(cv::Point3d(-0.42322458571123384, -0.40092165898617510, 0.58623004852443006));
points3d.push_back(cv::Point3d(-0.065169225135044417, -0.45710013122959070, -0.59439680166020692));
points3d.push_back(cv::Point3d(-0.58930631427961055, -0.14654377880184336, 0.037995544297616486));
points3d.push_back(cv::Point3d( 0.085421308023316114, 0.12211676381725516, 0.12859889522995691));
// Image 1
cv::Matx33d rotation1(-1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
0.0, 0.0, -1.0);
cv::Matx31d c1(0, 0, 5);
Matx31d tvec1 = -rotation1 * c1;
cv::Matx31d rvec1;
cv::Rodrigues(rotation1, rvec1);
// Image 2
cv::Matx33d rotation2(0.49999999999999983, -0.00000000000000000, 0.86602540378443871,
0.00000000000000000, 1.0000000000000000, 0.00000000000000000,
-0.86602540378443871, -0.00000000000000000, 0.49999999999999983);
cv::Matx31d c2(4.3301270189221936, 0, -2.4999999999999991);
Matx31d tvec2 = -rotation2 * c2;
cv::Matx31d rvec2;
cv::Rodrigues(rotation2, rvec2);
// project 3D points to images
std::vector<cv::Point2d> image1_points;
cv::projectPoints(points3d, rvec1, tvec1, cameraMatrix, distCoeffs, image1_points);
std::vector<cv::Point2d> image2_points;
cv::projectPoints(points3d, rvec2, tvec2, cameraMatrix, distCoeffs, image2_points);
// Solve for pose just to validate that rvec == rvec_calc and tvec == tvec_calc
cv::Matx31d tvec1_calc, rvec1_calc, tvec2_calc, rvec2_calc;
bool b1 = cv::solvePnP(points3d, image1_points, cameraMatrix, distCoeffs, rvec1_calc, tvec1_calc, false, SOLVEPNP_AP3P);
bool b2 = cv::solvePnP(points3d, image2_points, cameraMatrix, distCoeffs, rvec2_calc, tvec2_calc, false, SOLVEPNP_AP3P);
Second part is transforming the data to the new world frame W' using T
// random transformation homogeneous 4x4 matrix including scale
Matx33d trans_rot(0.12549613112731250, 0.73504921120164424, -0.66253649350437904,
0.33726020650278216, -0.65962968356110196, -0.66794121052375732,
-0.93032655622793992, -0.13997344290286745, -0.33151344030090363);
Matx44d trans(trans_rot(0,0), trans_rot(0,1), trans_rot(0,2), 0 ...