ArUco orientation using the function aruco.estimatePoseSingleMarkers()
Hi everyone!
I'm trying to program a python app that determine the position and orientation of an aruco marker. I calibrated the camera and everything and I used aruco.estimatePoseSingleMarkers that returns the translation and rotation vectors. The translation vector works fine but I don't understand how the rotation vector works. I took some picture to illustrate my problem with the "roll rotation":
Here the rotation vector is approximately [in degree]: [180 0 0]

Here the rotation vector is approximately [in degree]: [123 -126 0]

And here the rotation vector is approximately [in degree]: [0 -180 0]

And I don't see the logic in these angles. I've tried the other two rotations (pitch and yaw) and there appear also "random". So if you have an explication I would be very happy :)

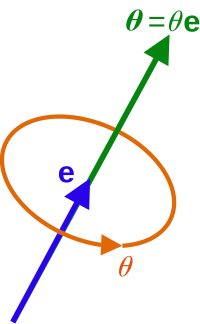
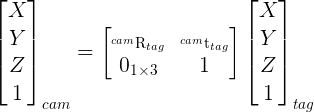
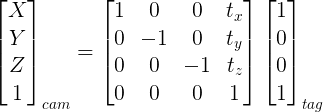
what does "is approximately [in degree]" mean ? you get an (exact) vector of 3 angles in rad.
Yes but I rounded and put them in degree to have a better idea of there meaning