Triangulation gives weird results for rotation

edit

OpenCV version 3.4.2

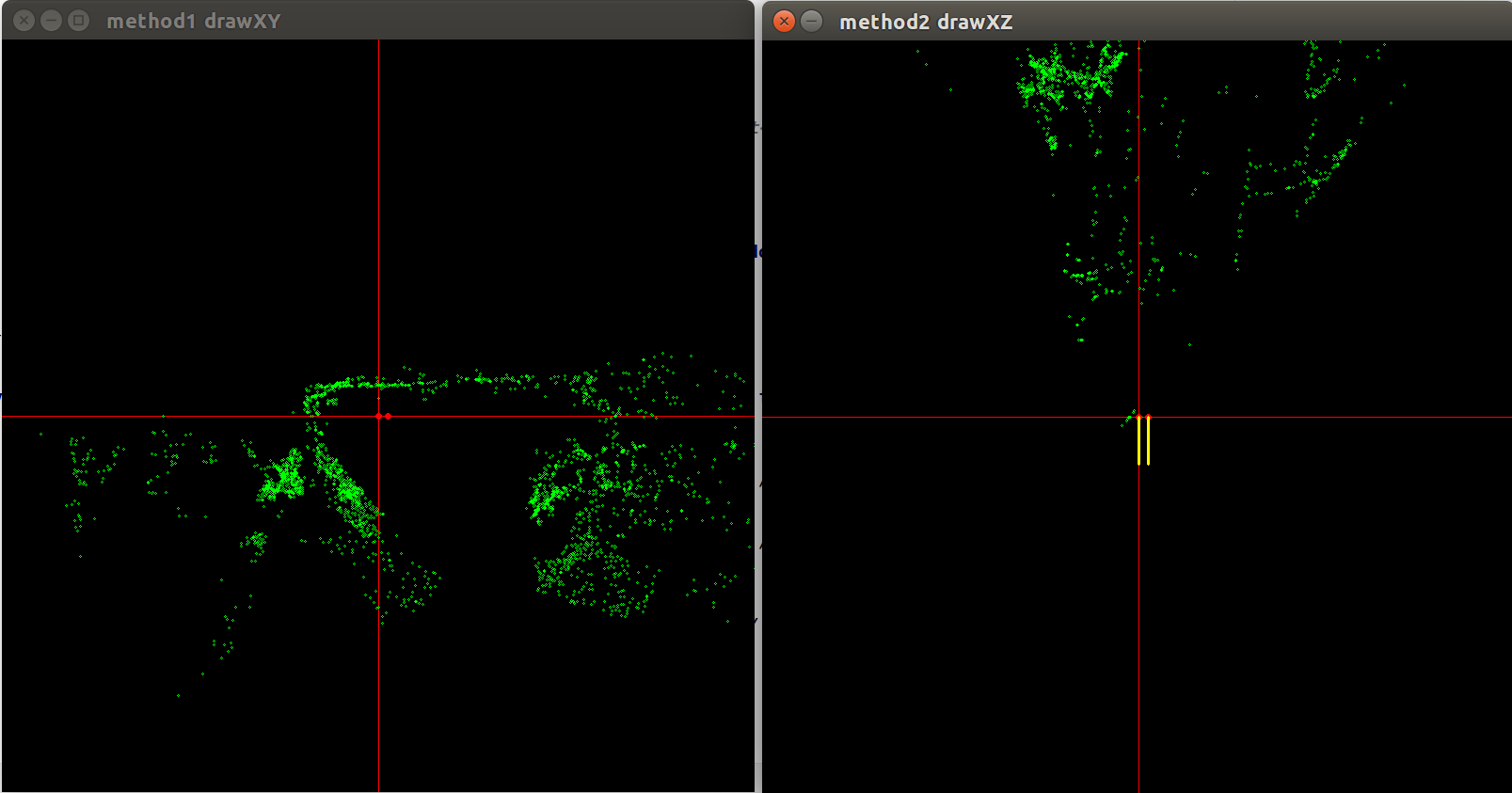
I am taking a stereo pair and using recoverPose to get the [R|t] pose of the camera, If I start at the origin and use triangulatePoints the result looks somewhat like expected although I would have expected the z points to be positive;

These are the poses of the cameras [R|t]

p0: [1, 0, 0, 0;
     0, 1, 0, 0;
     0, 0, 1, 0]

P1: [0.9999726146107655, -0.0007533190856300971, -0.007362237354563941, 0.9999683127209806;
     0.0007569149205790131, 0.9999995956157767, 0.0004856419317479311, -0.001340876868928852;
     0.007361868534054914, -0.0004912012195572309, 0.9999727804360723, 0.007847012372698725]

I get these results where the red dot and the yellow line indicates the camera pose (x positive is right, y positive is down):

When I rotate the first camera by 58.31 degrees and then use recoverPose to get the relative pose of the second camera the results are wrong.

Pose matrices where P0 is rotated by 58.31 degrees around the y axis before calling my code below.

P0: [0.5253219888177297, 0, 0.8509035245341184, 0;
     0, 1, 0, 0;
     -0.8509035245341184, 0, 0.5253219888177297, 0]

P1: [0.5315721563840478, -0.0007533190856300971, 0.8470126770406503, 0.5319823932782873;
     -1.561037994149129e-05, 0.9999995956157767, 0.0008991799591322519, -0.001340876868928852;
     -0.8470130118915117, -0.0004912012195572309, 0.5315719296650566, -0.8467543535708145]

(x positive is right, y positive is down)

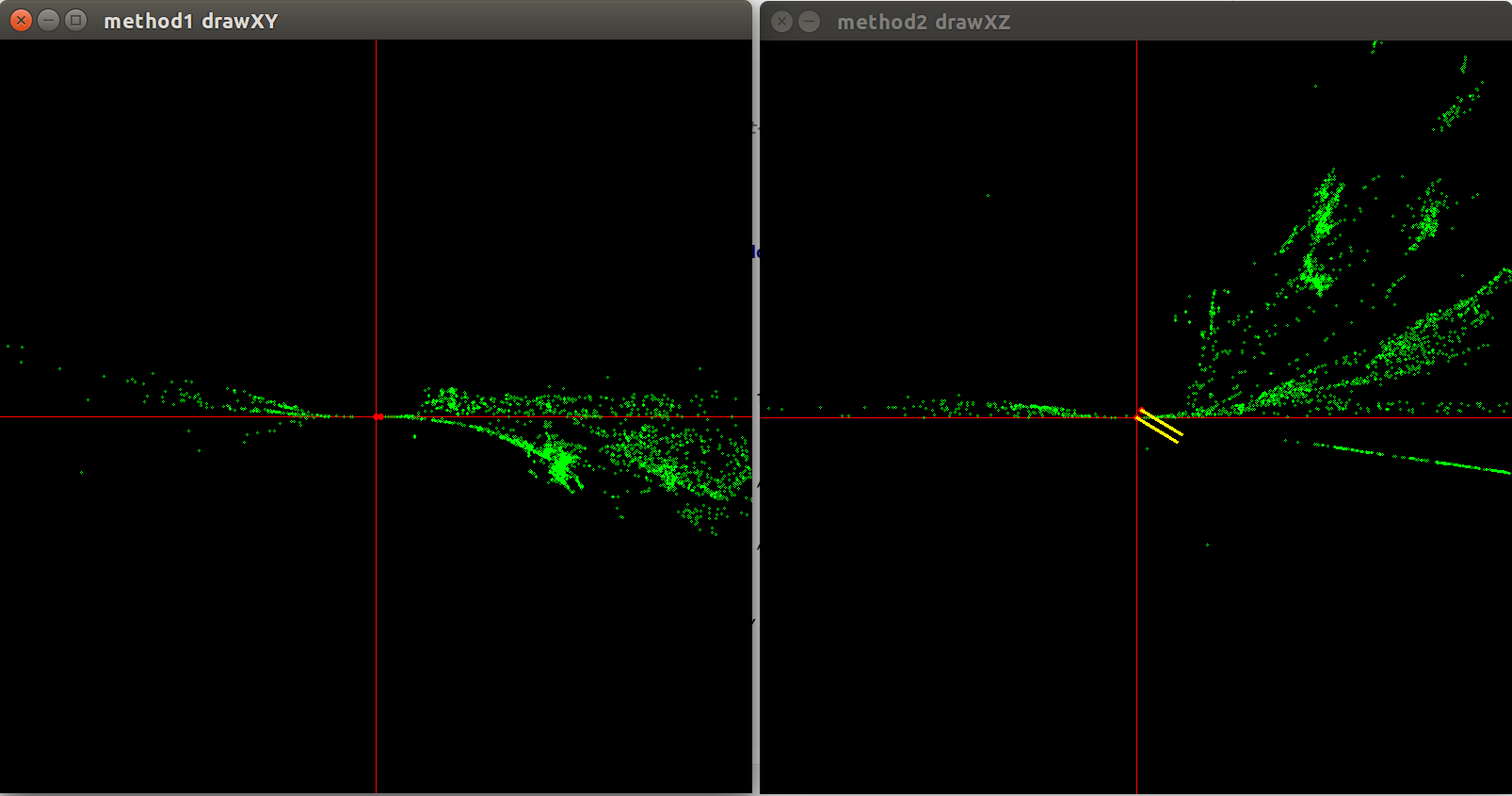
The pose of the second frame is calculated as follows:

new_frame->E = cv::findEssentialMat(last_frame->points, new_frame->points, K, cv::RANSAC, 0.999, 1.0, new_frame->mask);
int res = recoverPose(new_frame->E, last_frame->points, new_frame->points, K, new_frame->local_R, new_frame->local_t, new_frame->mask);
// https://stackoverflow.com/questions/37810218/is-the-recoverpose-function-in-opencv-is-left-handed 
// Convert so transformation is P0 -> P1
new_frame->local_t = -new_frame->local_t;
new_frame->local_R = new_frame->local_R.t();

new_frame->pose_t = last_frame->pose_t + (last_frame->pose_R * new_frame->local_t);
new_frame->pose_R = new_frame->local_R * last_frame->pose_R;
hconcat(new_frame->pose_R, new_frame->pose_t, new_frame->pose);

I then call triangulatePoints using the K * P0 and K * P1 on the corresponding points.

I feel like this is some kind of coordinate system issue as the points I would expect to have positive z values have a -z value in the plots and so the rotation is behaving strangely. I haven't been able to figure out what I need to do to fix it.

EDIT: Here is a gif of what's going on as I rotate through 360 degrees around Y. The cameras are still parallel. What am I missing, shouldn't the shape of the point cloud remain the same if both camera poses remain in relative positions even thought they have been rotated around the origin? Why are the points squashed into the X axis?