Is undistortPoints so noisy or is calibration the problem?

edit

Hi,

I am trying to do a sparse stereo reconstruction. I am currently trying out a "synthetic" experiment to find out how much noise I get in the 3D reconstruction given "perfect" landmark detection data.

The steps:

1. I take intrinsics I got from 2 real cameras. (The cameras have a resolution of 1600 x 1200)
2. I place the cameras "virtually" 40 cm apart. Both look in the same direction (Identity matrix on rot)
3. I define a couple of 3d points around 1.30m in front of the cameras.
4. I use projectpoints to get 2d image points for each camera.
5. I use undistort points on the 2d image points. (I put in the intrinsics as last argument of the function to get the 2d points in "pixel coordinates")
6. I use the undistorted 2d points to triangulate 3d points.

Then I measure the the error between the original points 3d points and the triangulated (l2 distance).

Results (in mm): Given the following distortion coefficients of the two cameras: distL = [-0.5844; 0,401; 0 ; 0 -0,2274] distR = [-0,6186; 0,2751; 0; 0; 0,03579]

I get error of 16 to 22 mm in the 3d reconstruction of points close to the frame of one of the camera images. I get 3 mm on points whose imagepoint counterparts lie a little more near the center.

When I make distortion coefficients all zero the reconstruction is more or less perfect.

This leads me to the assumption that undistortPoints is very instable and major source of noise. If you get that much nosie after single reconstruction step, I can not imagine how SfM can work. Especially if you think that in a real system also landmark detection will be a major source of error. Furthermore there are many published results on stereo reconstruction that have nearly micro meter precision.

Are the distortion coefficients shown above somehow degenerate? The calibration values I got, came from a real calibration procedure. I got a rms of 2.1 pixels (which is probably bad). But I thought that if I use these values in a "virtual environment" it should not matter what values they have, isnt it?

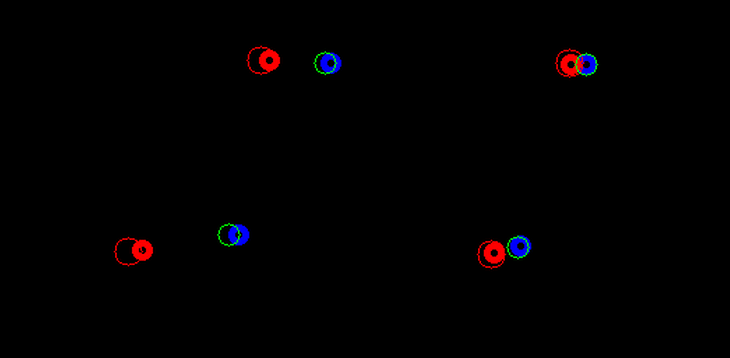
In the picture you can see the view of the "right" camera (where the points lie more towards the frame of the camera)

Blue points are projected perfect 3d coordinates with lense distortion

Green points are the projections of the triangulated points with lense distortion

Thick red are projected perfect 3d coordinates WHITOUT lense distortion (a ground truth for undistort).

Thin red are projected perfect 3d coordinates after undistortion.