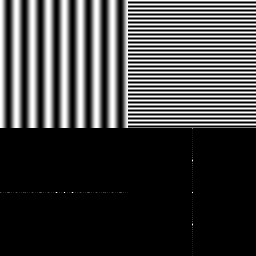
Fourier Transforms: Depict an image's variance?
I'm trying to understand Fourier transforms. If I convert a spatial domain image to the frequency domain using a Fourier transform.
- Does a Fourier transformed image depict/find the variances (intensity/colour/brightness change) over an image?
- In OpenCV, when I perform the FT I get a Mat/image back. Do the coordinates in that FT image correspond exactly to the original spatial image? For example, the pixel at location
[10,100]on the original image can be found at location[10,100]on the FT image. And that pixel value on the FT image represents the variance of that pixel?