derivation for perspective transformation matrix (Q)
Hi,
Opencv uses a perpective transformation matrix Q to convert pixels with disparity value into the corresponding [x, y, z] using the reprojectImageTo3D function. After searching on this site for a bit I found out that the matrix Q is as follows:
Q = |1 0 0 -Cx
|0 1 0 -Cy
|0 0 0 f
|0 0 -1/Tx (Cx - Cx')/Tx
I looked for equations to derive this but couldn't find any. I know about these matrix equations:
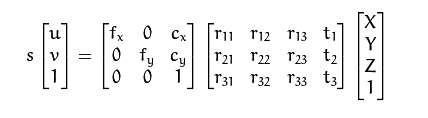
Is there a way to work back/invert this to get the matrix form of Q or am I missing something?
edit: projection matrices are the follows:
Pright = |F skew Cx F*Tx
|0 Fy Cy 0
|0 0 1 0
and a similar one for Pleft without the Tx factor. I guess what I'm looking for is a derivation from the projection matrix Pright to the reprojection matrix Q. I would assume there's an inversion or something to get from one to the other.
Thank you

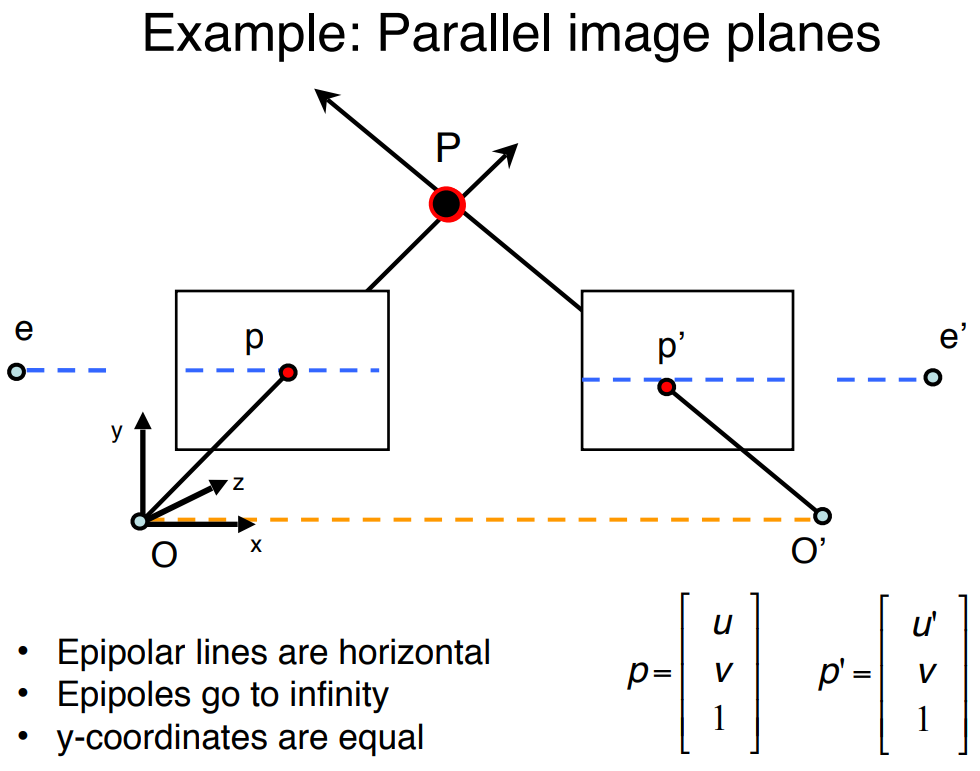
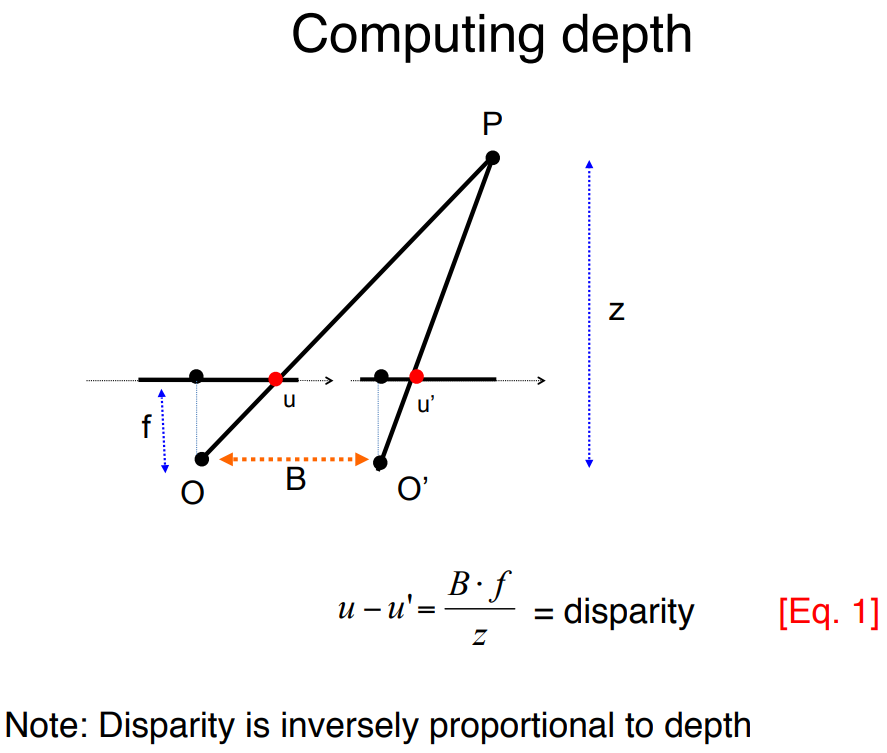
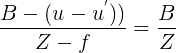
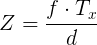
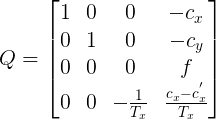

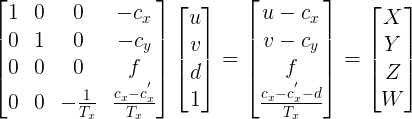
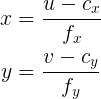
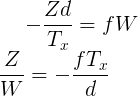
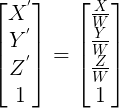
I thnik you can find your answer here