0

derivation for perspective transformation matrix (Q)

asked 2018-03-26 11:05:49 -0600

2ros0
76 ●2 ●4 ●10

updated 2018-03-28 12:22:17 -0600

Hi,

Opencv uses a perpective transformation matrix Q to convert pixels with disparity value into the corresponding [x, y, z] using the reprojectImageTo3D function. After searching on this site for a bit I found out that the matrix Q is as follows:

Q = |1 0 0 -Cx
    |0 1 0 -Cy
    |0 0 0 f
    |0 0 -1/Tx (Cx - Cx')/Tx

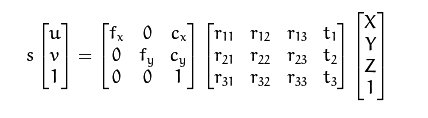
I looked for equations to derive this but couldn't find any. I know about these matrix equations: image description

Is there a way to work back/invert this to get the matrix form of Q or am I missing something?

edit: projection matrices are the follows:

Pright = |F skew Cx F*Tx
         |0 Fy Cy 0
         |0 0 1 0

and a similar one for Pleft without the Tx factor. I guess what I'm looking for is a derivation from the projection matrix Pright to the reprojection matrix Q. I would assume there's an inversion or something to get from one to the other.

Thank you

edit retag flag offensive close merge delete

Comments

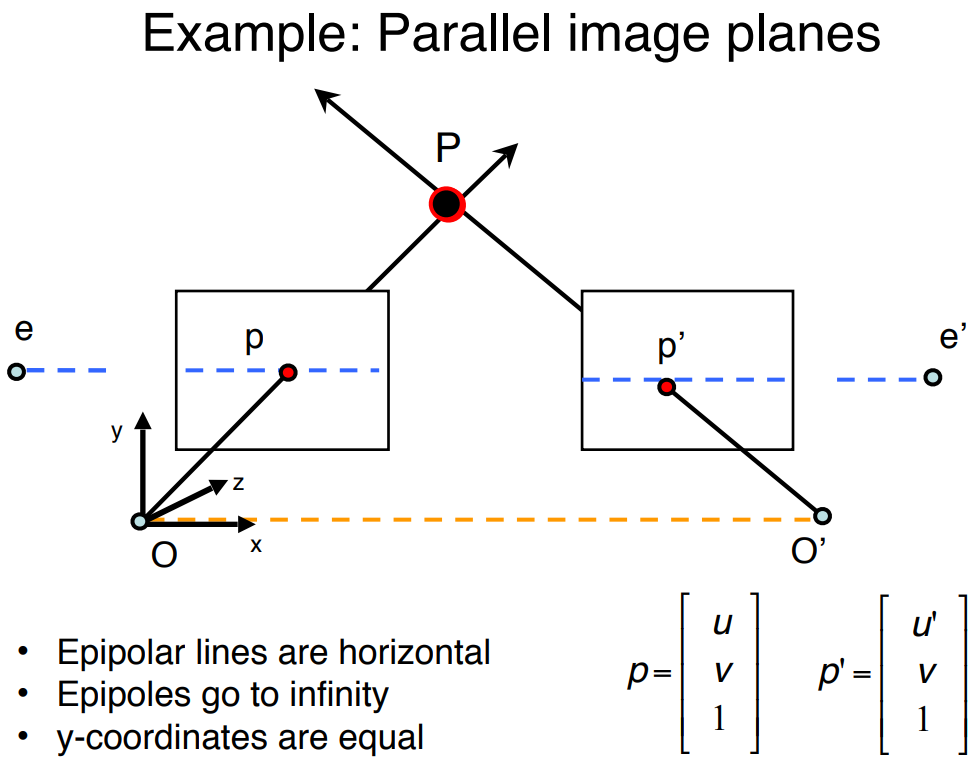
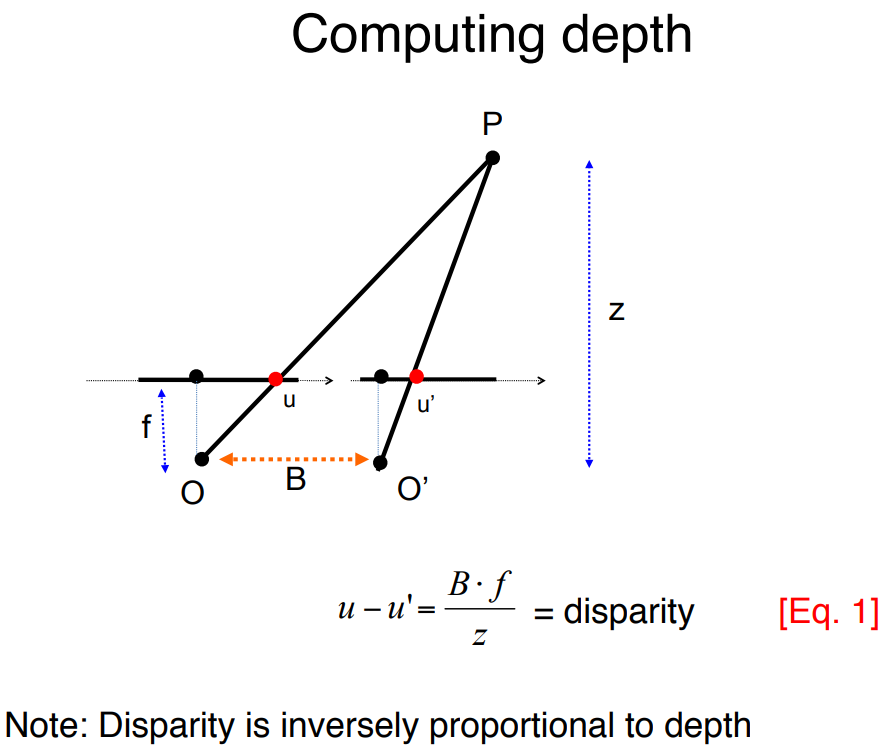
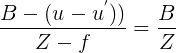
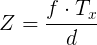
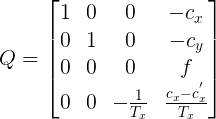
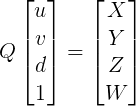
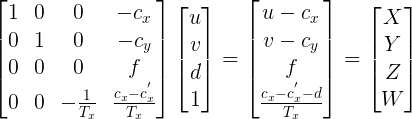
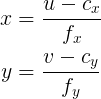
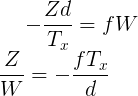
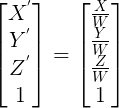
I thnik you can find your answer here

LBerger ( 2018-03-26 11:29:00 -0600 )edit

1 answer

Sort by » oldest newest most voted

4

answered 2018-03-28 15:14:31 -0600

Eduardo
3589 ●1 ●15 ●41

Please refer to the following references for more information:

CS231A · Computer Vision: from 3D reconstruction to recognition, Silvio Savarese
Lecture 6 - Stereo Systems Multi-view geometry, Silvio Savarese
Computer Vision: Algorithms and Applications, Richard Szeliski
Learning OpenCV 3 - Computer Vision in C++ with the OpenCV Library, Gary Bradski, Adrian Kaehler
[...]

Rectification will make the left and right images fronto-parallel:

Relation between depth of a triangulated point and disparity is the following:

From equation:

eq1

you will get [Eq. 1].

In OpenCV notation, depth of a triangulated point is calculated with:

eq2

The 4x4 disparity-to-depth mapping matrix Q is:

eq3

The relation between 3D point in homogeneous coordinate and disparity is:

eq4

eq5

Remember that 2D image point expressed in pixel can be converted to meter in the normalized camera frame (Z=1) with:

eq6

If left principal point c_x and right principal point c'_x are equals, we get the original equation to compute the depth:

eq7

Minus sign should come from if you compute d = (u - u') or d = (u' - u).

As everything is in homogeneous coordinate, 3D point is retrieved with:

eq8

edit flag offensive delete link

Links

Question Tools

2 followers

Stats

Asked: 2018-03-26 11:05:49 -0600

Seen: 7,670 times

Last updated: Mar 28 '18

Related questions

Copyright OpenCV foundation, 2012-2018. Content on this site is licensed under a Creative Commons Attribution Share Alike 3.0 license.

Powered by Askbot version 0.10.2

here is how