Accessing ALL points of a contour
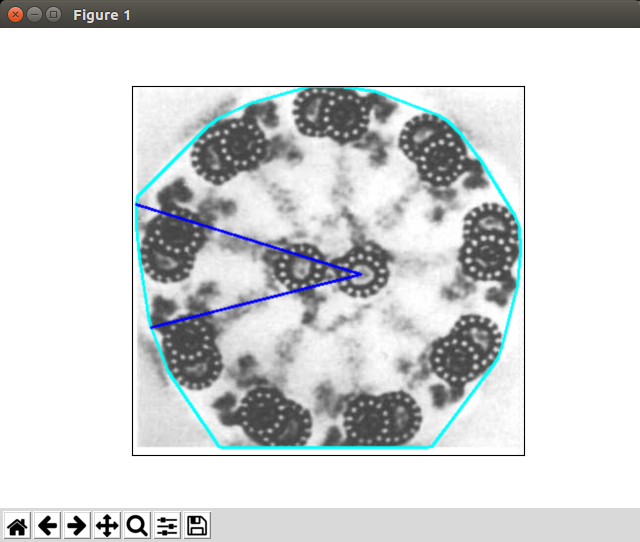
I made the exterior contour using the following:
def contoursConvexHull(contours):
pts = []
for i in range(0, len(contours)):
for j in range(0, len(contours[i])):
pts.append(contours[i][j])
pts = np.array(pts)
result = cv2.convexHull(pts)
return result
image = cv2.imread(args["image"])
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
blurred = cv2.GaussianBlur(gray, (5,5), 0)
thresh = cv2.threshold(blurred, 60, 255, cv2.THRESH_BINARY)[1]
imageCanny = cv2.Canny(blurred, 100, 200, 3)
img, contours, hierarchy = cv2.findContours(imageCanny, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
ConvexHullPoints = contoursConvexHull(contours)
cv2.polylines(image, [ConvexHullPoints], True, (0,255,255), 2)
and accessed the center of the contour using the following:
c = max(contours, key = cv2.contourArea)
M = cv2.moments(c)
if M["m00"] != 0:
cX = int(M["m10"] / M["m00"])
cY = int(M["m01"] / M["m00"])
print (cX,cY)
else:
cX, cY = 0,0
print (cX,cY)
My questions: 1. Since my image is not continuous, am I right in using convexHull and polylines() to draw the contour? 2. If I am right in using the above functions, how can I access ALL the points on the convexHull contour? Currently, if I use
cpts = []
cpts.append(ConvexHullPoints)
cpts = np.array(cpts)
print (cpts)
to see the points, I only get an array of 35 points.

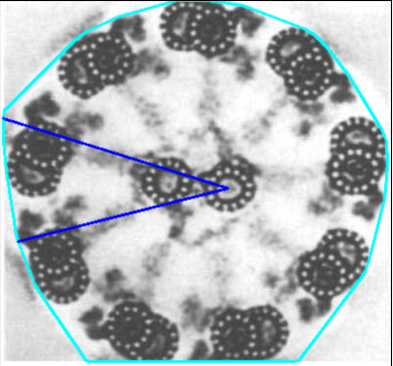

your convex hull just has a few points (the "corners", if you want so.) looking at it, i'd even expect less than 35, more like 12 points.
why do you think, there should be more ? again, it's the hull, not a contour.
Thanks for the comment! What confuses me, is that since all points on the image are not connected, how can I make a contour surrounding just the image? (similar to what the hull gives, but a contour)
sorry, i don't understand, what you're trying to achieve here.
I am trying to see all the black doublets in a straight line. I have tried using toPolar() but it gives me a distorted image like this. Since this approach didn't work well, I am now trying to extract each doublet (which will be contained in a "pizza slice" like shape, centered at the center of the image) and place them next to each other.