Mismatch of the Eigen Vector & Value
Hello,
I need to retrieve the eigen vector from a matrix. The problem is I don't match the result same as my matlab code.
I have a matrix symmetric 100x100 and trying to obtain eigen value and eigen vector from it. I work with double matrix (CV_64F) to have the best precision as possible (Already tried Float and it fail more).
My eigen value seems good but the vector loses some accuracy for each value ( Ex : value 1 to 25 exactly match with matlab but further you get to 100 , more I am losing precision, but I can work with that.)
But the problem is more with the eigen vector. The result is same as eigen value, lose precision but the problem is with the sign. If I take the firsts 25x25 results. I'm totally matching with matlab but randomly have positive or negative value. So I got wrong information at the end.
Right now I'm using cv:eigen function like this :
cv::eigen(oResultMax,oMatValue,oMatVector);
I have already tried the SelfAdjointSolver from the library Eigen. Eigen SelfAdjointSolver
Anyone have an idea ? Or suggest me something ?
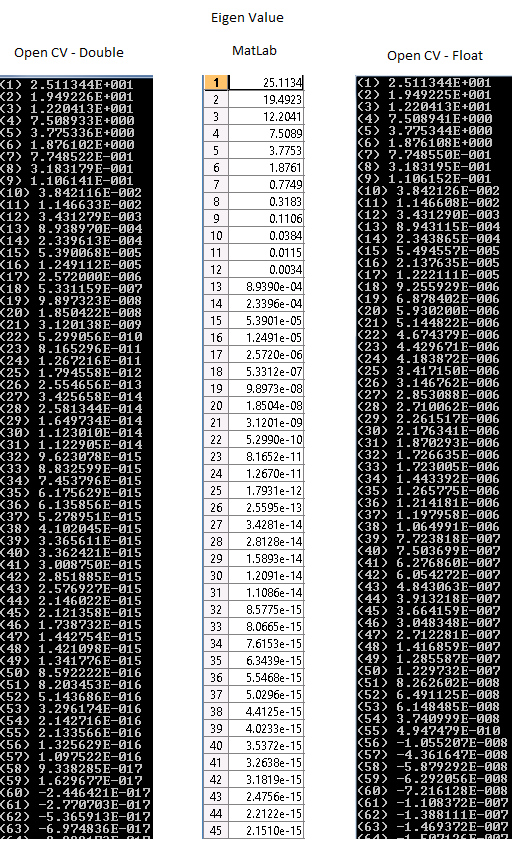
EDIT : (Add image of result)
Here you can see the image of the eigen value. If you refere to the MatLab result, the double result are almost same till the 27th and for the float till 14th.
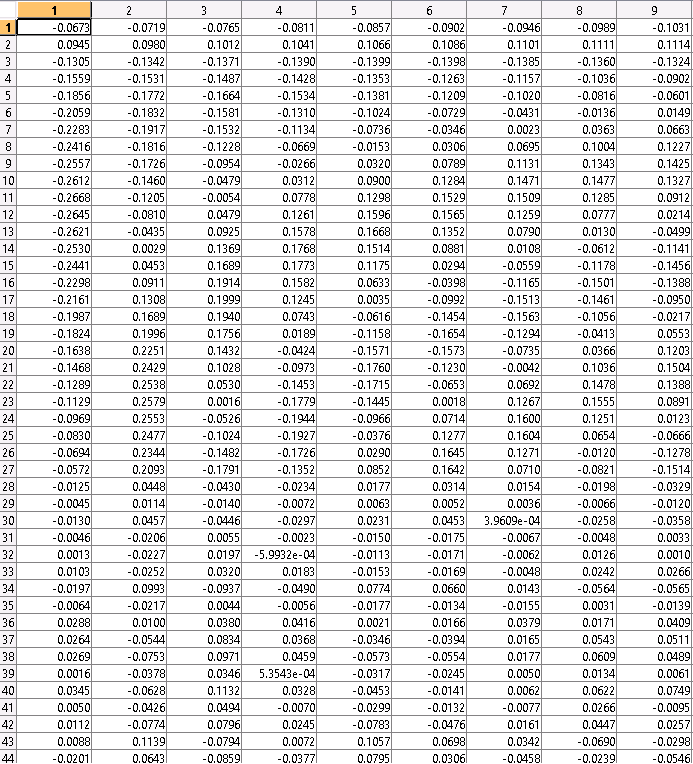
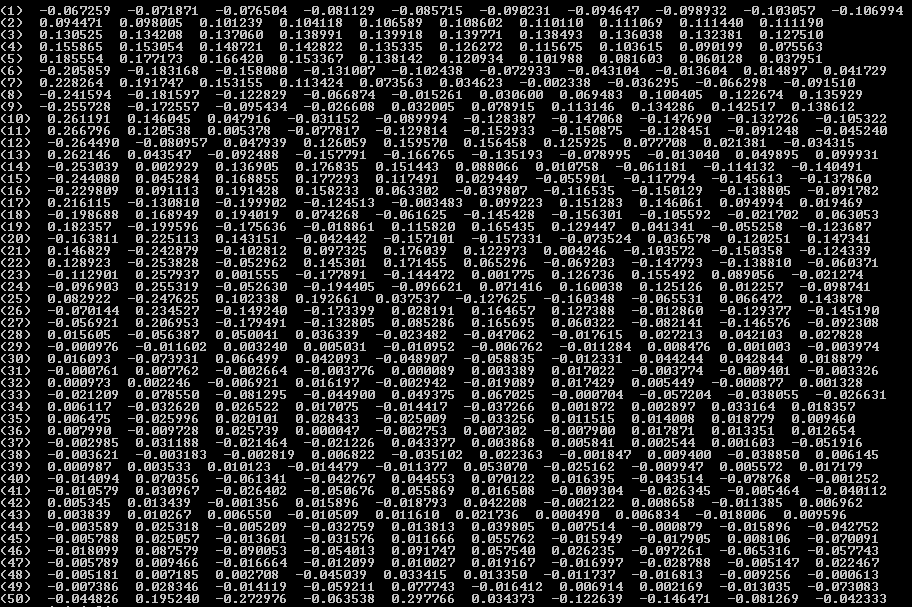
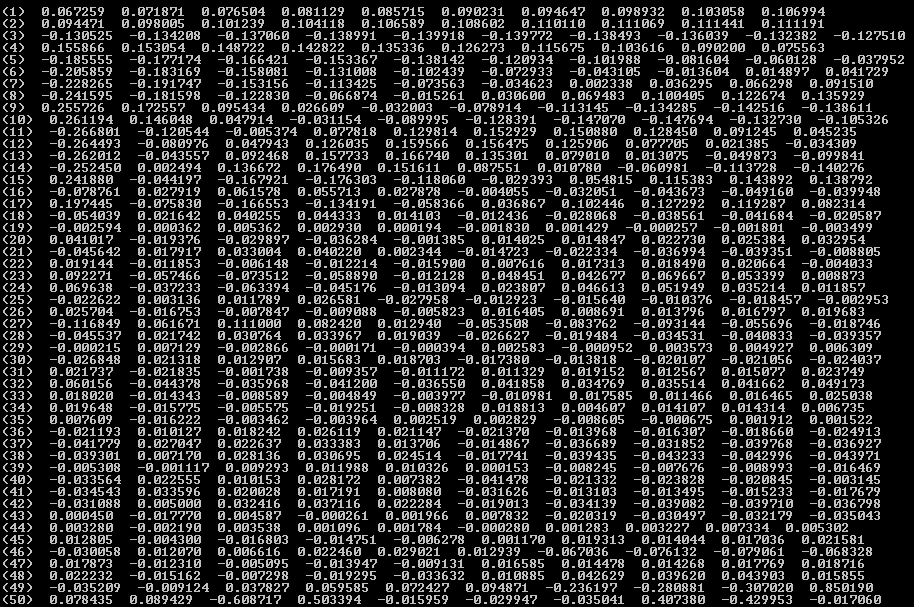
And those Image, you have Eigen Vector in order : MatLab , OpenCV Double and OpenCV Float.
As you can see double matching until 35th and float until 15th. And the sign of the result are differente from Matlab, Double and Float



Try doing a SVD with cv::SVD::compute, because for a symmetric matrix the singular values in W are square roots of eigenvalues.
Thanks Philipp, the problem is because I need to get Eigen Vector. I know with eigen values, I can obtain the vector but more processing. But can be an idea to try it.
I tried the SVD function and in same time, I tried PCA one (Suggested Eigen reference). My result for SVD are same as Eigen losing accuracy and sign problem. With PCA, the result are really not matching and looks more bad than my float with eigen. Both function were a good idea to try but they are not the answer to my problem. Thanks Philipp.