Revision history [back]

all the helper functions to calculate intersection point of two lines are exist in min_enclosing_triangle.cpp

but unfortunately you should implement all of them in JAVA

to determine if a line and polygon are intersecting you could iterate all points of polygon as pairs and test if any point pairs (line) is intersecting with the line ( sorry for my poor english. feel free to ask if I did not express well )

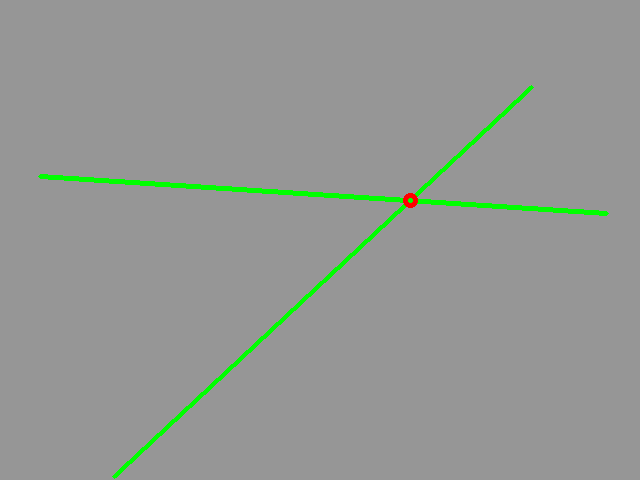
#include "opencv2/imgproc.hpp"
#include "opencv2/highgui.hpp"
#include <iostream>

using namespace cv;
using namespace std;

#define EPSILON 1E-5

static bool almostEqual(double number1, double number2);
static double distanceBtwPoints(const cv::Point2f &a, const cv::Point2f &b);


//! Compute the distance between two points
/*! Compute the Euclidean distance between two points
*
* @param a Point a
* @param b Point b
*/
static double distanceBtwPoints(const cv::Point2f &a, const cv::Point2f &b)
{
    double xDiff = a.x - b.x;
    double yDiff = a.y - b.y;

    return std::sqrt((xDiff * xDiff) + (yDiff * yDiff));
}

//! Check if one point lies between two other points
/*!
* @param point             Point lying possibly outside the line segment
* @param lineSegmentStart  First point determining the line segment
* @param lineSegmentEnd    Second point determining the line segment
*/
static bool isPointOnLineSegment(const cv::Point2f &point, const cv::Point2f &lineSegmentStart,
                                 const cv::Point2f &lineSegmentEnd)
{
    double d1 = distanceBtwPoints(point, lineSegmentStart);
    double d2 = distanceBtwPoints(point, lineSegmentEnd);
    double lineSegmentLength = distanceBtwPoints(lineSegmentStart, lineSegmentEnd);

    return (almostEqual(d1 + d2, lineSegmentLength));
}

//! Return the maximum of the provided numbers
static double maximum(double number1, double number2, double number3)
{
    return std::max(std::max(number1, number2), number3);
}

//! Check if the two numbers are equal (almost)
/*!
* The expression for determining if two real numbers are equal is:
* if (Abs(x - y) <= EPSILON * Max(1.0f, Abs(x), Abs(y))).
*
* @param number1 First number
* @param number2 Second number
*/
static bool almostEqual(double number1, double number2)
{
    return (std::abs(number1 - number2) <= (EPSILON * maximum(1.0, std::abs(number1), std::abs(number2))));
}

//! Determine the intersection point of two lines, if this point exists
/*! Two lines intersect if they are not parallel (Parallel lines intersect at
* +/- infinity, but we do not consider this case here).
*
* The lines are specified by a pair of points each. If they intersect, then
* the function returns true, else it returns false.
*
* Lines can be specified in the following form:
*      A1x + B1x = C1
*      A2x + B2x = C2
*
* If det (= A1*B2 - A2*B1) == 0, then lines are parallel
*                                else they intersect
*
* If they intersect, then let us denote the intersection point with P(x, y) where:
*      x = (C1*B2 - C2*B1) / (det)
*      y = (C2*A1 - C1*A2) / (det)
*
* @param a1 First point for determining the first line
* @param b1 Second point for determining the first line
* @param a2 First point for determining the second line
* @param b2 Second point for determining the second line
* @param intersection The intersection point, if this point exists
*/
static bool lineIntersection(const cv::Point2f &a1, const cv::Point2f &b1, const cv::Point2f &a2,
                             const cv::Point2f &b2, cv::Point2f &intersection)
{
    double A1 = b1.y - a1.y;
    double B1 = a1.x - b1.x;
    double C1 = (a1.x * A1) + (a1.y * B1);

    double A2 = b2.y - a2.y;
    double B2 = a2.x - b2.x;
    double C2 = (a2.x * A2) + (a2.y * B2);

    double det = (A1 * B2) - (A2 * B1);

    if (!almostEqual(det, 0))
    {
        intersection.x = static_cast<float>(((C1 * B2) - (C2 * B1)) / (det));
        intersection.y = static_cast<float>(((C2 * A1) - (C1 * A2)) / (det));

        return true;
    }

    return false;
}

int main (int argc,char **argv)
{
    RNG& rng = theRNG();
    int key = 0;

    while( key != 27 )
    {
        Mat test(480,640,CV_8UC3,Scalar(150,150,150));
        int ImageWidth = test.cols;
        int ImageHeight = test.rows;

        Point2f a1 = Point(rng.uniform(0,ImageWidth),rng.uniform(0,ImageHeight));
        Point2f b1 = Point(rng.uniform(0,ImageWidth),rng.uniform(0,ImageHeight));
        Point2f a2 = Point(rng.uniform(0,ImageWidth),rng.uniform(0,ImageHeight));
        Point2f b2 = Point(rng.uniform(0,ImageWidth),rng.uniform(0,ImageHeight));
        Point2f intersection;

        bool intersected = lineIntersection( a1, b1, a2, b2, intersection );
        cout << a1 << endl;
        cout << b1 << endl;
        cout << a2 << endl;
        cout << b2 << endl;
        cout << intersection << endl;

        line(test,a1,b1,Scalar(0,255,0));
        line(test,a2,b2,Scalar(0,255,0));

        if(isPointOnLineSegment(intersection,a1,b1) & isPointOnLineSegment(intersection,a2,b2))
        {
            circle(test,intersection,3,Scalar(0,0,255));
        }

        imshow("Line Intersection Test",test);
        key = waitKey(0);
    }
    return 0;
}