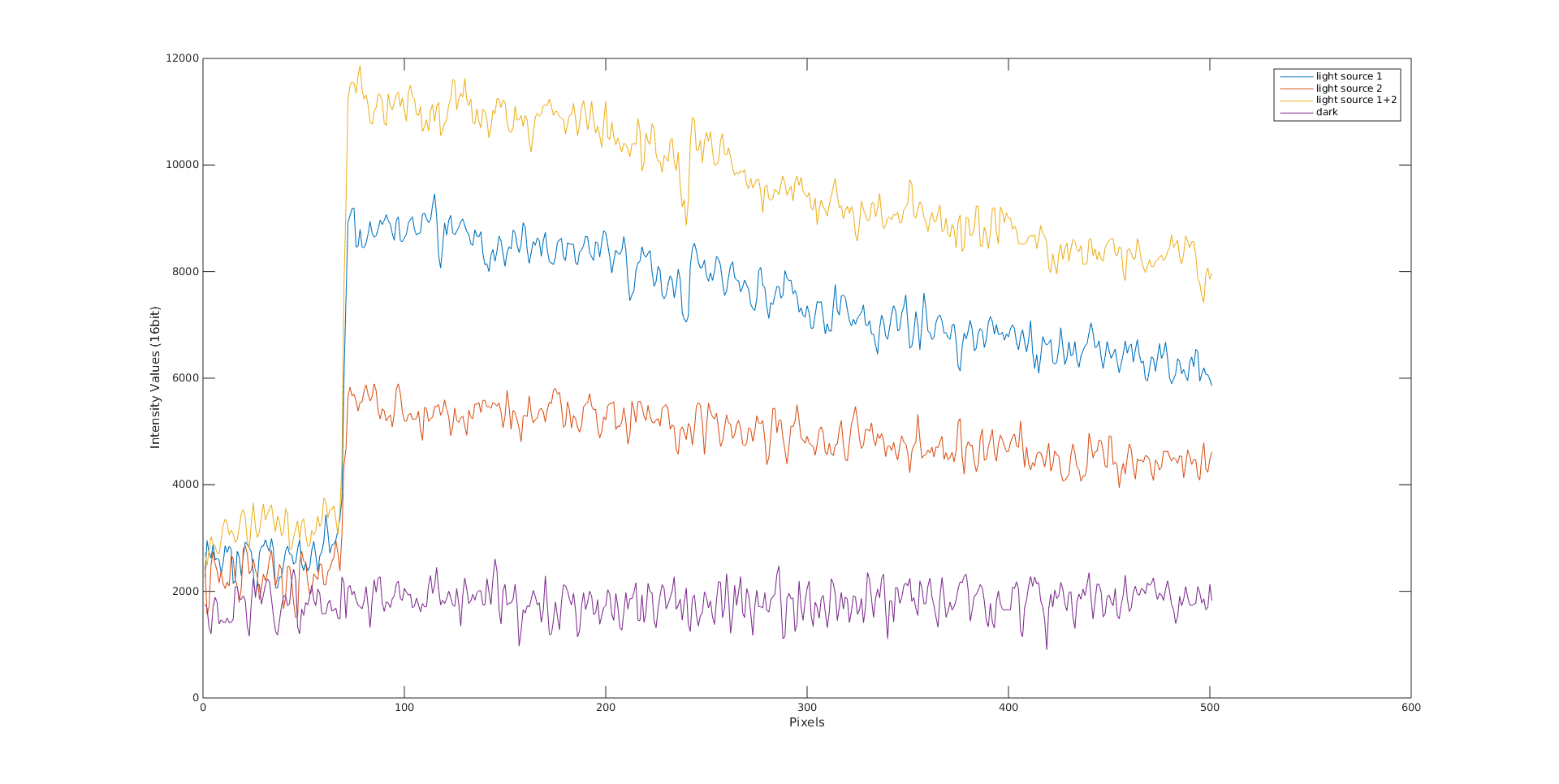
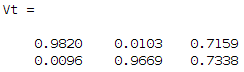
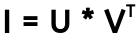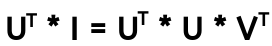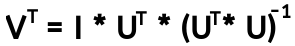Hi, lastly I am questioning the linearity and additivity of light propagation in images. As the title says I would like to see what is the contribution of light to image pixel intensity values and if the linearity and additivity of light is a valid assumption to be done or not. For that reason I established the following experiment. Imagine a room , where I set up a camera in top view (i.e. birds eye view) with two light sources of same type and light installed on two of the room corners. Then I took some images where the room was dark, i.e. light sources switched off (really hard to achieve that in reality since always there is gonna be a kind of light that the camera sensor can receive, but lets consider that I managed to do that), then only the first light source was switched on, then only the second light source was switched on and finally when both lights were switched on. These images were captured in rgb 8-bit depth (normal images normal images that can be acquired with a cheap camera sensor) with auto-setting fixed (i.e. exposure, gain, white-balance, etc...). Then I took 500 pixels and plotted their pixel intensity values for a case of one light source, second light source, both light sources and dark:
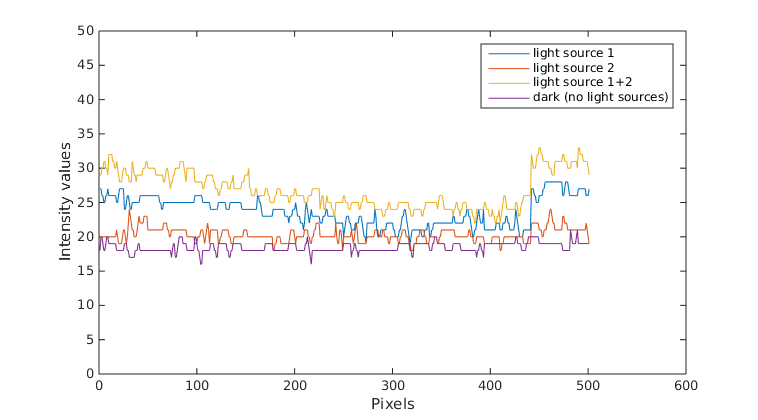
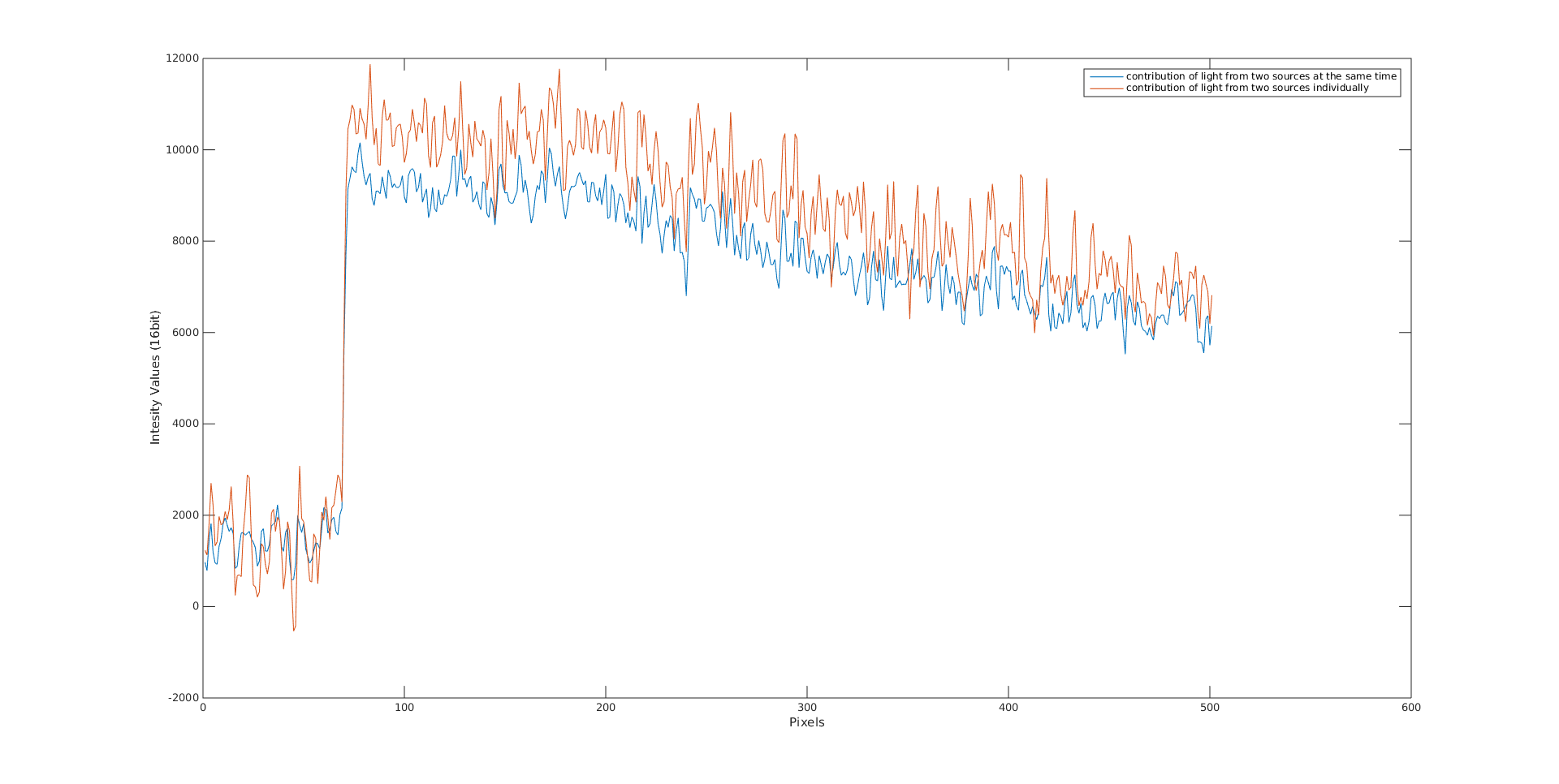
from the above image what you can observe is that I have a lot of noise when the lights are off (purple graph, ideally this should be close to zero). Then if we consider that the light works additive (in the simpler case) then the yellow graph should be as much higher from the blue graph as the blue from the orange graph respectively (again this in the ideal case). However, it is not you can see that in the plot below:
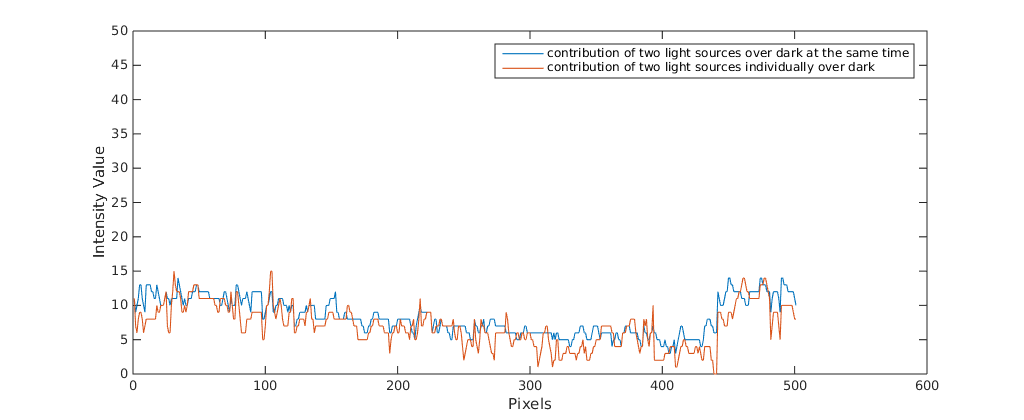
what you see here is
blue graph = yellow - purple (from the first graph)
orange graph = (blue - purple) + (orange - purple)
and these two ideally should be equal if additivity was the case, however we can say that they have a kind of similar pattern. However, it is obvious that what I am doing is not working. Then I searched a bit further and I found 
@pklab I know that you are working with different camera setups, so I do not know if you have some experience in such a subject. If you have I would be glad to hear any suggestions. Of course anyone that might have a clue is welcome to contribute to the discussion.
Thanks.