Hello,
I am working on ball tracking.
So far, using a calibrated camera, i have segmented a court area and segmented the ball from the background.
We know the dimensions of the court and the ball.
The court was segmented and a homography transform gives us a handle of remapping it. Using the homography, i can map back to the court model.
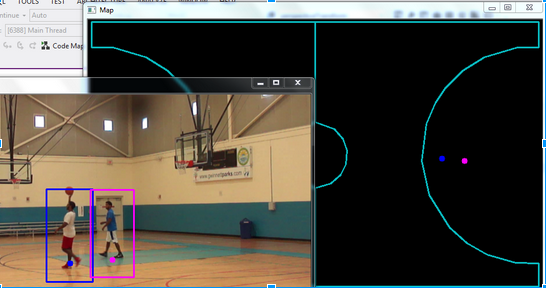
I want to do the same. Since the ball bounces, we need to use it's diameter to determine it's distance from the camera. Homography doesn't work for a bouncing ball.
Treating the ball as a 2D circle of diameter 23.44 cm. Using this, it's quite easy to use solvePNP to get the rotation/translation matrices for the object. But this is in 'camera space'.
Now, i guess we want to match up the homography transform and the rvec/tvec of solvePNP.
Expected Result: As above, the ball can be mapped to the court model for a 'top down' view of it's position.
If i used a court model and applied solvePNP, then i would have rvec/tvec for the court also in the same space as the ball. How do i get metric values? How do i get the co-ordinates of the ball as an x/y location on the court surface?
Regards,
Daniel

