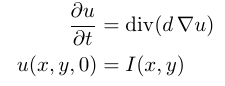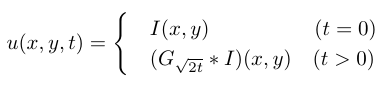I want to apply the denoising filter I named in the title which is based on the following equations:
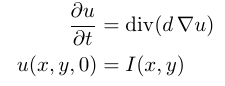
where d is a scalar constant diffusivity parameter, I(x, y) is the initial noisy image, and u(x, y, t)
is the image obtained after a diffusion time t lets say 5, 10 and 30. However, I am quite confused about which function to use and how, in order to achieve this in OpenCV. I have the feeling that it is quite simple but for some reason I am confused. Does anyone have an idea?
Here is a sample image:

UPDATE
this is the result images after following @LBerger 's code. They code, they are in time t = 0/t = 4 and d = 1:


, is it expected to be like that:

 that?
that?
I think that something is wrong. Because wrong, because I am trying also to compare it with the gaussian smoothing. And according to the following formula:
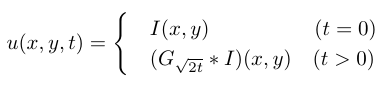
where G√2t (x, y) is the Gaussian kernel. This proves that performing isotropic linear diffusion for a time t with d = 1 is exactly equivalent to performing Gaussian smoothing with a σ = √(2t)
and applying the gaussian filter with the following code:
void gaussian_2D_convolution(const cv::Mat& src, cv::Mat& dst, const float sigma, const int ksize_x = 0, const int ksize_y = 0)
{
int ksize_x_ = ksize_x, ksize_y_ = ksize_y;
// Compute an appropriate kernel size according to the specified sigma
if (sigma > ksize_x || sigma > ksize_y || ksize_x == 0 || ksize_y == 0)
{
ksize_x_ = (int)ceil(2.0f*(1.0f + (sigma - 0.8f) / (0.3f)));
ksize_y_ = ksize_x_;
}
// The kernel size must be and odd number
if ((ksize_x_ % 2) == 0)
{
ksize_x_ += 1;
}
if ((ksize_y_ % 2) == 0)
{
ksize_y_ += 1;
}
// Perform the Gaussian Smoothing
GaussianBlur(src, dst, Size(ksize_x_, ksize_y_), sigma, sigma, BORDER_DEFAULT);
// show result
std::ostringstream out;
out << std::setprecision(1) << std::fixed << sigma;
String title = "sigma: " + out.str();
imshow(title, dst);
imwrite("gaussian/" + title + ".png", dst);
waitKey(260);
}
and calling it with gaussian_2D_convolution(img, smoothed, sqrt(2*5)); the two results of gaussian smoothing and isotropic linear smoothing in time t = 5 are respectively:


which are for sure not similar :-(.