Hi all,
I have a binary image containing objects similar to the ones to the left in the figure below. I would now like to perform some operation to get to the shapes to the right (or the corresponding contour). The red dot represents a starting point if it would be necessary for the workflow (preferentially not).
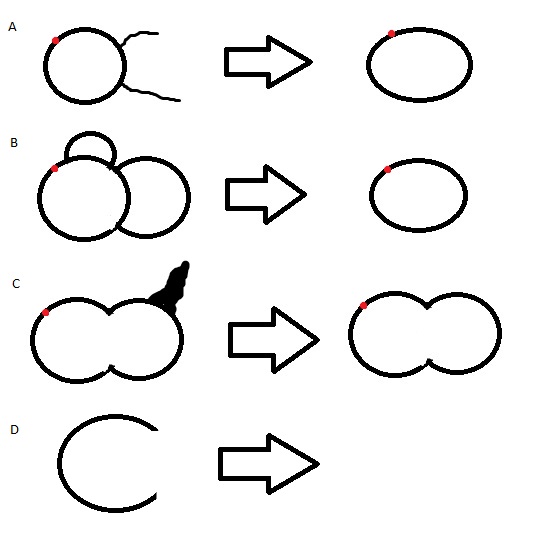
A) and B) illustrates that I would like to remove parts outside of the "largest enclosed area", basically the interior of the circle
In C) this area would be larger because there is no line between the circles (and I drew some thick part to illustrate that this is not based on the contours but on the binary image)
D) shows that if there is no "enclosed area" it shouldn't return anything
Any suggestion on how to approach this would be very much appreciated!
Some stuff I've thought about is: -Flood fill from different starting points and keep largest region -Some graph theory method about enumerating circular paths and then select among them -Start by "eroding" the shape from the outside according to some rules until only the interior region remains -Cleverly cut the shape and keep track of the intersections and thereby deduce something -Maybe it can be gotten from the contour function somehow?
This is somewhat time critical, so faster approaches would be better than slower
Thanks!


