I'm working on video stabilization topic. At the smoothing part, I need smooth parameters (translation, rotation+scale) by using B-spline curve for warping in order to create stabilized video.
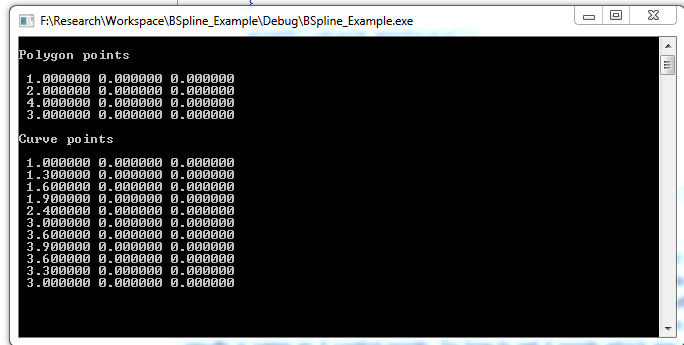
Now, I am testing on some points. For example, I have 4 points (control points) with degree = 2, after using b-spline I wanna obtain 4 smoothed points. But when I use B-spline curve sample code in below, it created more than 4 points. I can not understand exactly that those results points which are belong to original points (control points). If I only get 4 points, the results is like as 4 original points (4 control points).How to get 4 smoothed points by using B-Spline curve?
Hope you guys help me to show this problem.
Here is the code.
#include "stdafx.h"
#include <stdio.h>
#include <conio.h>
/*
Subroutine to generate a B-spline open knot vector with multiplicity
equal to the order at the ends.
c = order of the basis function
n = the number of defining polygon vertices
nplus2 = index of x() for the first occurence of the maximum knot vector value
nplusc = maximum value of the knot vector -- $n + c$
x() = array containing the knot vector
*/
void knot(int n, int c, int x[])
{
int nplusc,nplus2,i;
nplusc = n + c;
nplus2 = n + 2;
x[1] = 0;
for (i = 2; i <= nplusc; i++){
if ( (i > c) && (i < nplus2) )
x[i] = x[i-1] + 1;
else
x[i] = x[i-1];
}
}
/* Subroutine to generate B-spline basis functions for open knot vectors
C code for An Introduction to NURBS
by David F. Rogers. Copyright (C) 2000 David F. Rogers,
All rights reserved.
Name: basis.c
Language: C
Subroutines called: none
Book reference: p. 279
c = order of the B-spline basis function
d = first term of the basis function recursion relation
e = second term of the basis function recursion relation
npts = number of defining polygon vertices
n[] = array containing the basis functions
n[1] contains the basis function associated with B1 etc.
nplusc = constant -- npts + c -- maximum number of knot values
t = parameter value
temp[] = temporary array
x[] = knot vector
*/
void basis(int c,float t, int npts,int x[],float n[])
{
int nplusc;
int i,k;
float d,e;
float temp[36];
nplusc = npts + c;
/* calculate the first order basis functions n[i][1] */
for (i = 1; i<= nplusc-1; i++){
if (( t >= x[i]) && (t < x[i+1]))
temp[i] = 1;
else
temp[i] = 0;
}
/* calculate the higher order basis functions */
for (k = 2; k <= c; k++){
for (i = 1; i <= nplusc-k; i++){
if (temp[i] != 0)/* if the lower order basis function is zero skip the calculation */
d = ((t-x[i])*temp[i])/(x[i+k-1]-x[i]);
else
d = 0;
if (temp[i+1] != 0) /* if the lower order basis function is zero skip the calculation */
e = ((x[i+k]-t)*temp[i+1])/(x[i+k]-x[i+1]);
else
e = 0;
temp[i] = d + e;
}
}
if (t == (float)x[nplusc]){ /* pick up last point */
temp[npts] = 1;
}
/* put in n array */
for (i = 1; i <= npts; i++) {
n[i] = temp[i];
}
}
/*Subroutine to generate a B-spline curve using an uniform open knot vector
C code for An Introduction to NURBS
by David F. Rogers. Copyright (C) 2000 David F. Rogers,
All rights reserved.
Name: bspline.c
Language: C
Subroutines called: knot.c, basis.c, fmtmul.c
Book reference: Section 3.5, Ex. 3.4, Alg. p. 281
b[] = array containing the defining polygon vertices
b[1] contains the x-component of the vertex
b[2] contains the y-component of the vertex
b[3] contains the z-component of the vertex
k = order of the \bsp basis function
nbasis = array containing the basis functions for a single value of t
nplusc = number of knot values
npts = number of defining polygon vertices
p[,] = array containing the curve points
p[1] contains the x-component of the point
p[2] contains the y-component of the point
p[3] contains the z-component of the point
p1 = number of points to be calculated on the curve
t = parameter value 0 <= t <= 1
x[] = array containing the knot vector
*/
void bspline(int npts,int k,int p1,float b[],float p[])
{
int i,j,icount,jcount;
int i1;
int x[30]; /* allows for 20 data points with basis function of order 5 */
int nplusc;
float step;
float t;
float nbasis[20];
float temp;
nplusc = npts + k;
/* zero and re-dimension the knot vector and the basis array */
for(i = 0; i <= npts; i++){
nbasis[i] = 0.;
}
for(i = 0; i <= nplusc; i++){
x[i] = 0.;
}
/* generate the uniform open knot vector */
knot(npts,k,x);
icount = 0;
/*calculate the points on the bspline curve */
t = 0;
step = ((float)x[nplusc])/((float)(p1-1));
for (i1 = 1; i1<= p1; i1++){
if ((float)x[nplusc] - t < 5e-6){
t = (float)x[nplusc];
}
basis(k,t,npts,x,nbasis); /* generate the basis function for this value of t */
for (j = 1; j <= 3; j++){ /* generate a point on the curve */
jcount = j;
p[icount+j] = 0.;
for (i = 1; i <= npts; i++){ /* Do local matrix multiplication */
temp = nbasis[i]*b[jcount];
p[icount + j] = p[icount + j] + temp;
jcount = jcount + 3;
}
}
icount = icount + 3;
t = t + step;
}
}
void main()
{
int i;
int npts,k,p1;
float b[31]; /* allows for up to 10 control vertices */
float p[103]; /* allows for up to 100 points on curve */
npts = 4;
k = 2; /* second order, change to 4 to get fourth order */
p1 = 11; /* eleven points on curve */
for (i = 1; i <= 3*npts; i++){
b[i] = 0.;
}
for (i = 1; i <= 3*p1; i++){
p[i] = 0.;
}
/*
Define the control polygon, Ex. 3.4 in the z=1 plane because
this is three dimensional routine. x=b[1], y=b[2], z=b[3], etc.
*/
b[1]=1;
b[2]=0;
b[3]=0;
b[4]=2;
b[5]=0;
b[6]=0;
b[7]=4;
b[8]=0;
b[9]=0;
b[10]=3;
b[11]=0;
b[12]=0;
bspline(npts,k,p1,b,p);
printf("\nPolygon points\n\n");
for (i = 1; i <= 3*npts; i=i+3){
printf(" %f %f %f \n",b[i],b[i+1],b[i+2]);
}
printf("\nCurve points\n\n");
for (i = 1; i <= 3*p1; i=i+3){
printf(" %f %f %f \n",p[i],p[i+1],p[i+2]);
}
getch();
}