Hi everyone!
I'm beginner at OpenCV and Computer Vision.
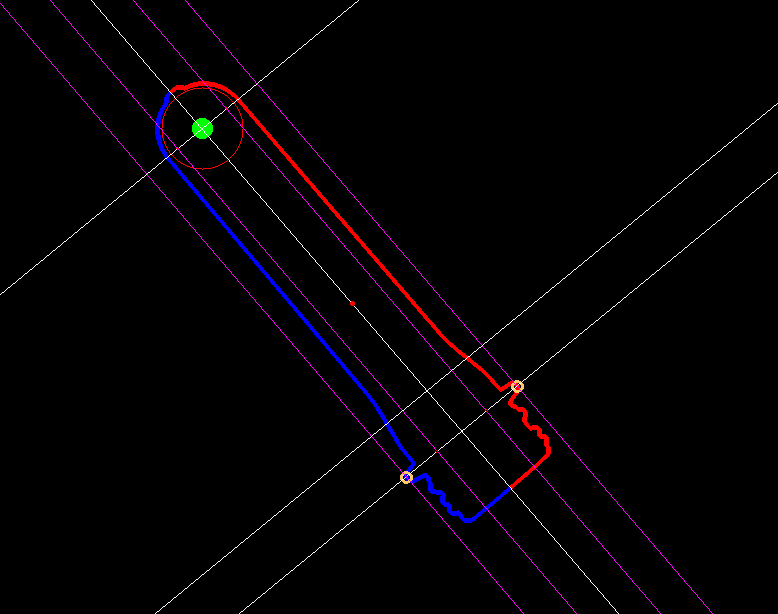
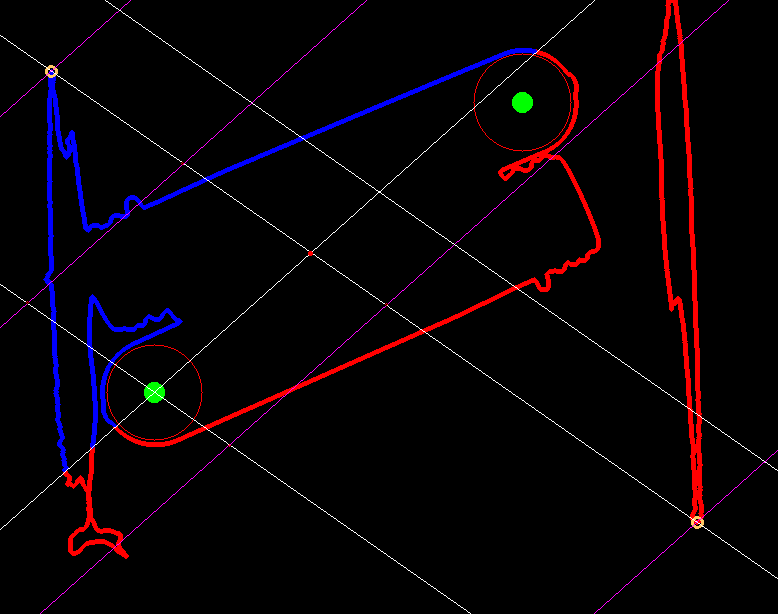
I need to solve the problem of separating connected preforms. I'm write code that allows me to handle a single preform fairly well, but if there are more than 1 of them, then there are problems, which you can see in the picture.
How can I solve this problem? I read about the waterfall, watershed, but its application did not give the desired result.
Source code
If u want u can get source image this: click
#include "mainwindow.h"
using namespace std;
using namespace cv;
// Найти уравнение прямой
void line_equation(Point src1, Point src2, double& k, int& b) {
if ((src1.x != src2.x) && (src1.y != src2.y)) {
k = (double) (src1.y - src2.y) / (double) (src1.x - src2.x);
b = src1.y - (k * src1.x);
} else {
k = 0;
}
}
void find_parallel(Point src, vector<Point>& dst, double k, int rows) {
int b = src.y - k * src.x;
dst.push_back(Point(-b/k, 0));
dst.push_back(Point((rows - b) / k, rows));
}
// Найти точки пересечения прямой и контура
void line_interseption(vector<Point> src_line, Point p, Point q, vector<Point>& dst_point) {
int d = 0;
bool first_point_flag = false;
bool second_point_flag = false;
for(size_t i = 1; i < src_line.size(); i++) {
d = abs((p.y - q.y)*src_line[i].x - (p.x - q.x)*src_line[i].y + p.x * q.y - p.y * q.x)
/sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
if(p.x != q.x) {
if((d == 0) && !first_point_flag && (p.x > src_line[i].x)) {
dst_point.push_back(src_line[i]);
first_point_flag = true;
}
if((d == 0) && !second_point_flag && (p.x < src_line[i].x)) {
dst_point.push_back(src_line[i]);
second_point_flag = true;
}
} else {
if((d == 0) && !first_point_flag && (p.y > src_line[i].y)) {
dst_point.push_back(src_line[i]);
first_point_flag = true;
}
if((d == 0) && !second_point_flag && (p.y < src_line[i].y)) {
dst_point.push_back(src_line[i]);
second_point_flag = true;
}
}
}
}
// Найти точку пересечения прямых
void intersection_points(Point flp1, Point flp2, Point slp1, Point slp2, Point& dst_point) {
double k1 = (double)(flp2.y - flp1.y) / (flp2.x - flp1.x);
double k2 = (double)(slp2.y - slp1.y) / (slp2.x - slp1.x);
double b1 = k1 * flp1.x - flp1.y;
double b2 = k2 * slp1.x - slp1.y;
dst_point.x = -(b1 - b2) / (k2 - k1);
dst_point.y = -(k2 * b1 - k1 * b2) / (k2 - k1);
}
// Найти максимально удаленную точку от прямой
void find_max(vector<Point> sepCont, Point p, Point q, Point &dst) {
dst = sepCont[0];
int d = 0;
int d_max = abs((p.y - q.y)*sepCont[0].x - (p.x - q.x)*sepCont[0].y + p.x * q.y - p.y * q.x)
/sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
for(size_t i = 1; i < sepCont.size(); i++) {
d = abs((p.y - q.y)*sepCont[i].x - (p.x - q.x)*sepCont[i].y + p.x * q.y - p.y * q.x)
/sqrt((p.y - q.y) * (p.y - q.y) + (p.x - q.x) * (p.x - q.x));
if(d > d_max) {
dst = sepCont[i];
d_max = d;
}
}
}
// Найти расстаяние между двумя точками
int find_dist(Point p1, Point p2) {
return sqrt((p2.x - p1.x) * (p2.x - p1.x) + (p2.y - p1.y) * (p2.y - p1.y));
}
// Найти точку на прямой
void point_on_line(Point src1, Point src2, double k, int b, Point& dst) {
double dif = 0;
if(src1.y - src2.y != 0) {
dif = (double)abs(src1.x - src2.x) / (double)abs(src1.y - src2.y);
} else {
dif = 2;
}
int dist = find_dist(src1, src2);
if(dif > 1) {
if(src1.x > src2.x) {
dst.y = k * (src1.x - dist/10) + b;
dst.x = src1.x - dist/10;
} else {
dst.y = k * (src1.x + dist/10) + b;
dst.x = src1.x + dist/10;
}
} else {
if(src1.y > src2.y) {
dst.y = src1.y - dist/10;
dst.x = (dst.y - b) / k;
} else {
dst.y = src1.y + dist/10;
dst.x = (dst.y - b) / k;
}
}
}
void point_on_line(vector<Point> src, double k, int b, vector<Point>& dst) {
double dif = 0;
if(src[0].y - src[1].y != 0) {
dif = (double)abs(src[0].x - src[1].x) / (double)abs(src[0].y - src[1].y);
} else {
dif = 2;
}
int dist = find_dist(src[0], src[1]);
if(dif > 1) {
if(src[0].x > src[1].x) {
dst[0].y = k * (src[0].x - dist/10) + b;
dst[0].x = src[0].x - dist/10;
dst[1].y = k * (src[1].x + dist/10) + b;
dst[1].x = src[1].x + dist/10;
} else {
dst[0].y = k * (src[0].x + dist/10) + b;
dst[0].x = src[0].x + dist/10;
dst[1].y = k * (src[1].x - dist/10) + b;
dst[1].x = src[1].x - dist/10;
}
} else {
if(src[0].y > src[1].y) {
dst[0].y = src[0].y - dist/10;
dst[0].x = (dst[0].y - b) / k;
dst[1].y = src[1].y + dist/10;
dst[1].x = (dst[1].y - b) / k;
} else {
dst[0].y = src[0].y + dist/10;
dst[0].x = (dst[0].y - b) / k;
dst[1].y = src[1].y - dist/10;
dst[1].x = (dst[1].y - b) / k;
}
}
}
// Извлечь прямоугольник по 4 точкам
void extractRect(Mat src, Mat dst, int min_y, int min_x, int max_y, int max_x,
int b1, int b2, int b3, int b4, double k1, double k2) {
while(min_y <= max_y) {
int x1 = (min_y - b3) / k1;
int x2 = (min_y - b1) / k2;
if(x1 < min_x)
x1 = (min_y - b2) / k1;
if(x2 > max_x)
x2 = (min_y - b4) / k2;
if(x1 > x2) {
int temp = x2;
x2 = x1;
x1 = temp;
}
for(int i = x1; i <= x2; i++) {
dst.at<uchar>(Point(i, min_y)) = src.at<uchar>(Point(i, min_y));
}
min_y++;
}
}
void separeteContour(vector<vector<Point>> src, vector<Point>& top, vector<Point>& low, double k, int b) {
for(size_t i = 0; i < src.size(); i++) {
for(size_t j = 0; j < src[i].size(); j++) {
int y_cont = k * src[i][j].x + b;
if(src[i][j].y < y_cont) {
low.push_back(src[i][j]);
} else {
top.push_back(src[i][j]);
}
}
}
}
int main()
{
Mat fg, bg, blured, preform, bin, ROI, erosion_dst, cont;
vector<vector<Point>> contours, true_cont;
Point2d vertices[4];
int b_main, b1, b2, b3, b4;
double k_main, k_peak;
bg = imread("C:\\2\\bg.bmp", IMREAD_GRAYSCALE);
fg = imread("C:\\2\\pf1.bmp", IMREAD_GRAYSCALE);
resize(fg, fg, Size(), 0.3, 0.3, INTER_AREA);
resize(bg, bg, Size(), 0.3, 0.3, INTER_AREA);
absdiff(fg, bg, preform);
threshold(preform, bin, 10, 255, THRESH_BINARY);
findContours(bin, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
uint32_t resolution = fg.rows * fg.cols;
uint32_t kernelSize = resolution < 1280 * 1280 ? 7:
resolution < 2000 * 2000 ? 15:
resolution < 3000 * 3000 ? 27:
45;
GaussianBlur(bin, blured, Size(kernelSize, kernelSize), 9, 9);
imshow("bin", bin);
imshow("pf", preform);
for(size_t i = 0; i < contours.size(); i++) {
if(contours[i].size() > 1000)
true_cont.push_back(contours[i]);
}
vector<Vec3f> circles;
HoughCircles(blured, circles, HOUGH_GRADIENT, 1, fg.rows/16, 100, 30, 1, 100);
Moments mnt = moments(true_cont[0]);
Point center_mass(mnt.m10/mnt.m00, mnt.m01/mnt.m00);
Point circle_center(cvRound(circles[0][0]), cvRound(circles[0][1]));
line_equation(center_mass, circle_center, k_main, b_main);
int main_dist = find_dist(center_mass, circle_center);
Point peak1, peak2;
vector<Point> top_cont, low_cont;
separeteContour(true_cont, top_cont, low_cont, k_main, b_main);
find_max(top_cont, center_mass, circle_center, peak1);
find_max(low_cont, center_mass, circle_center, peak2);
line_equation(peak1, peak2, k_peak, b1);
Point neck_point;
intersection_points(center_mass, circle_center, peak1, peak2, neck_point);
point_on_line(neck_point, center_mass, k_main, b_main, neck_point);
line(fg, Point(-b_main/k_main, 0), Point((fg.rows-b_main)/k_main, fg.rows), 255, 1);
vector<Point> neck_parallel;
vector<Point> circle_parallel;
vector<Point> circle_int;
vector<Point> circle_int_par1;
vector<Point> circle_int_par2;
find_parallel(neck_point, neck_parallel, k_peak, fg.rows);
find_parallel(circle_center, circle_parallel, k_peak, fg.rows);
line_interseption(top_cont, circle_parallel[0], circle_parallel[1], circle_int);
line_interseption(low_cont, circle_parallel[0], circle_parallel[1], circle_int);
b2 = circle_int[0].y - k_peak * circle_int[0].x;
point_on_line(circle_int, k_peak, b2, circle_int);
find_parallel(circle_int[0], circle_int_par1, k_main, fg.rows);
find_parallel(circle_int[1], circle_int_par2, k_main, fg.rows);
Point neck_int1, neck_int2;
intersection_points(circle_int_par1[0], circle_int_par1[1], neck_parallel[0], neck_parallel[1], neck_int1);
intersection_points(circle_int_par2[0], circle_int_par2[1], neck_parallel[0], neck_parallel[1], neck_int2);
vertices[0] = circle_int[0];
vertices[1] = circle_int[1];
vertices[2] = neck_int1;
vertices[3] = neck_int2;
circle(fg, neck_point, 2, 0, 2);
circle(fg, peak1, 2, 100, 2);
circle(fg, peak2, 2, 100, 2);
circle(fg, vertices[0], 2, 0, 2);
circle(fg, vertices[1], 2, 0, 2);
circle(fg, vertices[2], 2, 0, 2);
circle(fg, vertices[3], 2, 0, 2);
line(fg, neck_parallel[1], neck_parallel[0], 255, 1);
line(fg, circle_parallel[1], circle_parallel[0], 255, 1);
line(fg, circle_int_par1[1], circle_int_par1[0], 255, 1);
line(fg, circle_int_par2[1], circle_int_par2[0], 255, 1);
imshow("fg", fg);
imshow("pf", preform);
imshow("bl", blured);
waitKey();
return EXIT_SUCCESS;
}




