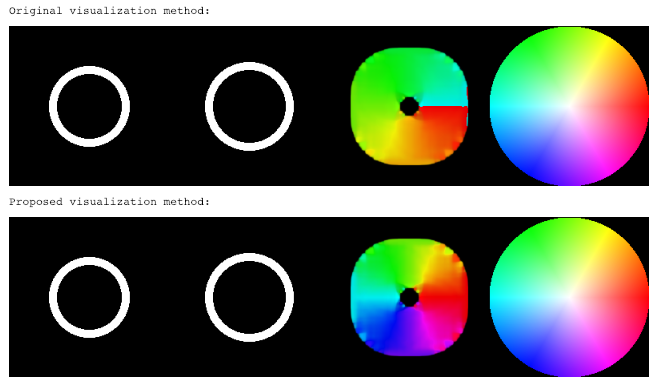
I believe the canonical optical flow example is the one provided at https://docs.opencv.org/master/d7/d8b/tutorial_py_lucas_kanade.html. It takes a flow angle, converted from Cartesian to polar, in the range (0, 2Pi) and converts it to hue by ang180/np.pi/2, producing hue in the range (0, 180). This doesn't make any sense to me. I think hue, as a polar entity itself, should fully encompass the direction of the flow, hence it should have the range (0, 360), which is simply achieved by ang180/np.pi.
I am very perplexed by this since the seemingly correct equation is actually the simpler option. Someone actually added an extra division by two, thereby breaking the equation (by my reasoning). Consequently, I am concerned I am misunderstanding this somehow. But if you run the optical flow algorithm on artificially generated data (painted rectangles offset in the four cardinal directions), you get much more sensible results using my recommended equation. Hue encompasses and utilizes the entire hue range and depicts smooth direction gradients. The existing example only utilizes half the available hue (from red to cyan), and worse than discarding half the hue availability, it also yields a discontinuity between directions 359 and 0, depicted as a sudden jump from cyan to red. This really doesn't make any sense.
How has this example stood for so long in this form? Further compounding my confusion, this apparent error has propagated to other projects, as shown at https://www.programcreek.com/python/example/89313/cv2.calcOpticalFlowFarneback. Consequently, as I stated above, I genuinely feel I am making some sort of mistake on all of this. I can't be the first person to have ever noticed this, so I must be interpreting it incorrectly, right? I'm very confused.
What does everyone else think about this?
Thanks.