I have a simple program that finds convex hulls and draws them onto my frame.
For my application, I am interested in one convex hull in particular shown below inside the labels S and V.
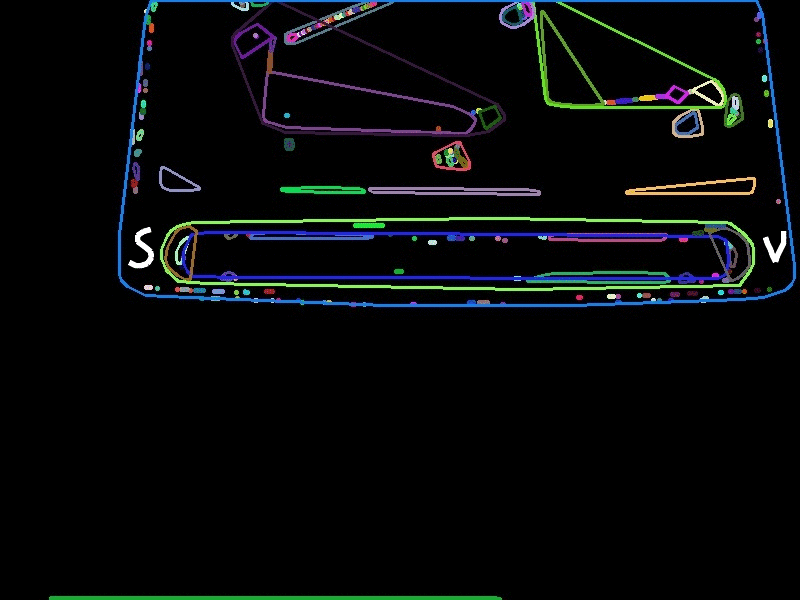
One way I thought of narrowing it down is looking for convex hulls which consist of parallel lines by performing a theta test for parallelism.
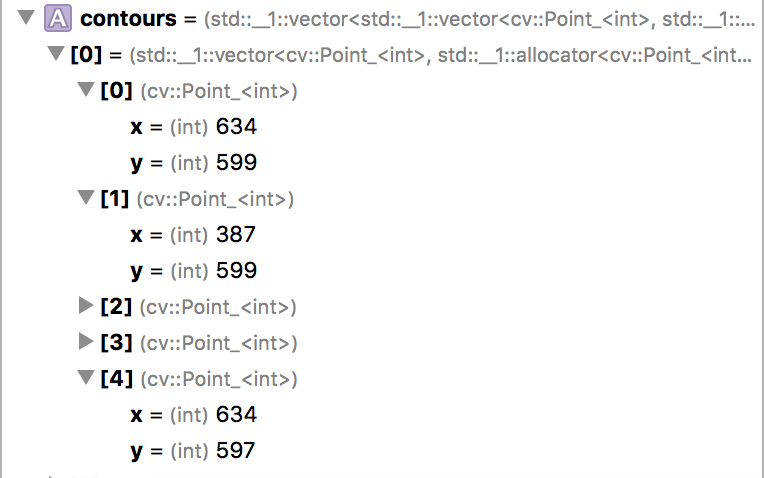
The structure returned by convexHull is of vector<vector<Point>>. Below is a sample image showing the points of one convex inside the container
My questions are:
- Is (634, 599)->(387, 599)->....->(634, 597)->(634, 599) the relation between the points? If no, what is then?
- Along with parallelism, length is another factor I had in mind to filter out useless convexes. Any better suggestions to detect this structure?
Any recommendations/responses are highly appreciated it!
Edit 1
Sample Image
Minimal Code
int main(int argc, const char * argv[])
{
Mat frame, grey, threshold, cannyEdge, gaussianBlur;
vector<vector<Point>> contours;
VideoCapture camera(0);
if(!camera.isOpened())
{
cerr << "Error grabbing the camera\n";
return -1;
}
while(true)
{
camera.read(frame);
cvtColor(frame, grey, COLOR_BGR2GRAY);
for(int mainIndex = 0; mainIndex <= 12; ++mainIndex)
{
int autoThreshold = 200 - 15 * mainIndex;
// TODO: tweak these values around
Canny(grey, cannyEdge, 25, 2*autoThreshold, 3, true);
GaussianBlur(cannyEdge, gaussianBlur, Size(3,3), 0);
findContours(gaussianBlur, contours, hierarchy, CV_RETR_LIST, CHAIN_APPROX_SIMPLE);
Mat contoursFrame = Mat::zeros(frame.size(), CV_8UC3);
Mat convexHullFrame = Mat::zeros(frame.size(), CV_8UC3);
convexes.resize(contours.size());
for(size_t index = 0; index < contours.size(); ++index)
{
convexHull(contours[index], convexes[index]);
}
cout << "Found " << thresholdCentres.size() << " circles at threshold " << autoThreshold << endl;
for(size_t index = 0; index < contours.size(); ++index)
{
Scalar colour = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255));
drawContours(contoursFrame, contours, int(index), colour, 2, LINE_8);
drawContours(convexHullFrame, convexes, int(index), colour, 2, LINE_8);
}
imshow("Convex", convexHullFrame);
imshow("Contours", contoursFrame);
}
char tappedKey = waitKey(1);
if(tappedKey == 27)
{
break;
}
}
destroyAllWindows();
camera.release();
return 0;
}



