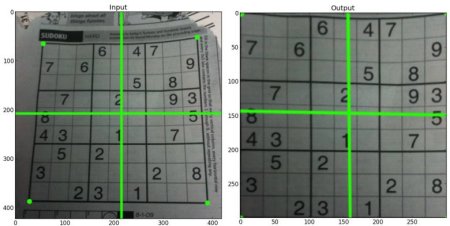
I'm a bit confused in whether something can be accomplished or not.
Supposing I have 2 identical delimiting shapes:
Rectangle, 5 units height, 50 units width.
Which I position on a uniform plane parallel to each other so that they form a rectangle between them. Can I obtain the perspective transformation needed to go from what a video camera sees (perspective view) to a 2D representation of it?
Based on this link: (docs.opencv.org/3.0-beta/doc/py_tutorials/py_imgproc/py_geometric_transformations/py_geometric_transformations.html)
I need to specify 4 points for the input, and another 4 points for the output.
The input 4 points are known, since I can detect the top left/right corners of my top marker, and the bottom left/right corners of my bottom marker.
The problem lies in the 4 points required for the output. I know what the width of the final image should be (which is equal to my marker width) but i don't know what the height should be (as the markers CAN be positioned with a variable distance between each other).
Is there a way to calculate this distance somehow? (I somehow believe there must be an alternative to using the intrinsic/extrinsic matrices since I know before hand the dimensions of both of my markers.)