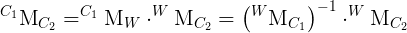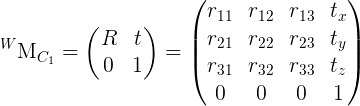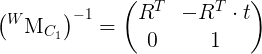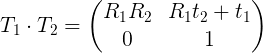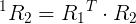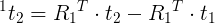How to derive relative R and T from camera extrinsics

edit

Hi,

I have an array of cameras capturing a scene. They are precalibrated and their coordinates are stored as translation from scene origin, and 3 Euler angles describing the camera's orientation.

I need to supply stereoRectify() the relative translation and rotation of the second camera with respect to the first camera. I have found several contradictory definitions of R and T, none of which seem to give me a correct rectified image (epipolar lines are not horizontal).

With trial and error, the following (still probably incorrect) is the closest I've been able to get:

R = R₁ * R₂^T

T = R^T * ( T₁ - T₂ )

Where R₁ and R₂ are 3x3 rotation matrices formed from the Euler angles, and T₁ and T₂ are translation vectors from the scene origin. R and T are then sent to stereoRectify() once R has been converted to axis-angle notation with Rodrigues().

I have also tried R = R₂ * R₁^T with T = R₁ * ( T₂ - T₁ ), along with a few other permutations. All incorrect.

If I could get the real way to obtain R and T from world-space, that would help immensely with identifying the source of the incorrect outputs I'm getting.

I have taken into account the z-foward and -y up coordinate system of OpenCV. I have also rendered a pair of CGI images to verify that incorrect calibration was not the issue. (My goal is to compute the disparity map between each camera (taken as pairs), in order to later perform derive depth maps and perform image-based view synthesis.)

Thanks a million!
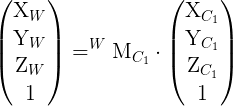
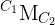