World Co-ordinates and Object Co-ordinates
Hello,
I am working with cv::SolvePnp(), cv::ProjectPoints(). We are working with a fully calibrated camera with known camera matrix and distortion coefficients.
Given a detected marker, it is possible to get the rvec and tvec for a given 3D model.
This has been done for two types of model, a board model and a ball model. We then get three sets of tvecs/rvecs, one for the board and then two more models for the balls. As shown below.....
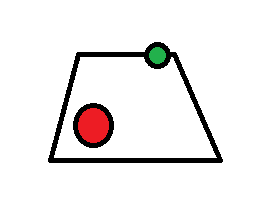
How do we relate these? We can project the model points into the image usings the result of solvepnp.
How do the rvecs and tvecs relate in this case? Is it possible to get the location of each ball on the board in terms of it's x,y,z location relative to the board model?
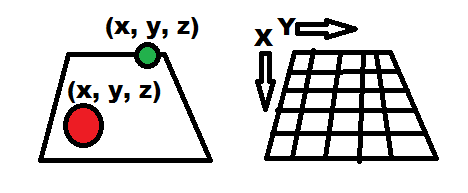
The board is shaped as (0,0), (1,0), (1,1), (0,1).
The ball are circles centered at 0, with radius 0.1, which is in scale with the real world objects.
Process so far....
- Detect board corners.
- Detect ball locations, and fit a circle.
- Calculate rvecs and tvecs for board and the two balls.
- Use projectPoints to project model into image.
Can we get more information on where the balls are on the board? The ultimate aim is collision detection/prediction once locations and velocity are determined.
Kind regards,
Daniel

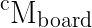
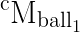 and
and 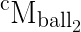 ,
,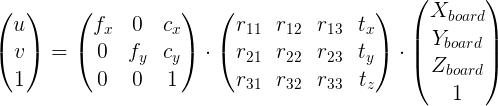 ,
,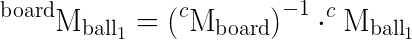
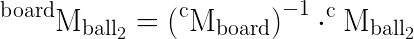 .
.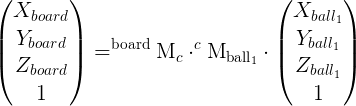
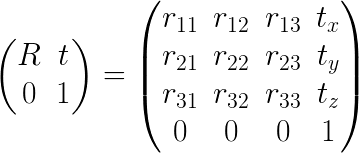
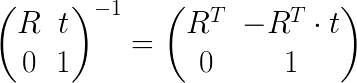
Awesome. I think that is exactly what i need. What is this process called? How do i find out more about it?
You mean homogeneous transformation matrix ?
To inverse an homogeneous transformation matrix (page 10) (R | t ; 0 | 1), you can use the formula: (R | t ; 0 | 1)^-1 = (Rt | -Rt.t ; 0 | 1)
@Eduardo Why you don't convert your comment to answer ? @MRDaniel if it's works please accept the answer... thank you
@Eduardo@pklab Yup, i am happy to mark this as the correct answer! :)