Theory behind estimating rotation in motion_estimators.cpp (CalcRotation)

edit

I am trying to understand the theory behind parts of the stitching pipeline in order to support not only camera rotation, but translation as well. The relevant part of the code is in /modules/stitching/src/motion_estimators.cpp (lines 60pp):

CalcRotation(int _num_images, const std::vector<MatchesInfo> &_pairwise_matches, std::vector<CameraParams> &_cameras)
    : num_images(_num_images), pairwise_matches(&_pairwise_matches[0]), cameras(&_cameras[0]) {}

void operator ()(const GraphEdge &edge)
{
    int pair_idx = edge.from * num_images + edge.to;

    Mat_<double> K_from = Mat::eye(3, 3, CV_64F);
    K_from(0,0) = cameras[edge.from].focal;
    K_from(1,1) = cameras[edge.from].focal * cameras[edge.from].aspect;
    K_from(0,2) = cameras[edge.from].ppx;
    K_from(1,2) = cameras[edge.from].ppy;

    Mat_<double> K_to = Mat::eye(3, 3, CV_64F);
    K_to(0,0) = cameras[edge.to].focal;
    K_to(1,1) = cameras[edge.to].focal * cameras[edge.to].aspect;
    K_to(0,2) = cameras[edge.to].ppx;
    K_to(1,2) = cameras[edge.to].ppy;

    Mat R = K_from.inv() * pairwise_matches[pair_idx].H.inv() * K_to;
    cameras[edge.to].R = cameras[edge.from].R * R;
}

In this part of the code the stitcher tries to estimate the camera parameters between two views "from" and "to". (The input is a graph of matching images and estimated homographies are given). I understand the code assumes constant intrinsic parameters. Estimated calibration parameters are used to set up K_from and K_to, the intrinsic calibration parameters of the two views.

Next, extrinsic parameters are estimated with the core assumption that cameras do not translate! In Szeliski - Computer Vision: Algorithms and Applications (9.1.3 Rotational panoramas) the relation between the extrinsic parameters and the homography between the two views is explained:

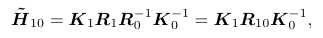
I try to derive the last two lines of the code based on this formula. For simplicity I (assume and) define

K0 := K_from, K1 := K_to, R0 := cameras[edge.from].R, R1 := cameras[edge.to].R

Here we go (starting with what the algorithm is doing)

cameras[edge.to].R = cameras[edge.from].R * K_from.inv() * pairwise_matches[pair_idx].H.inv() * K_to:

R1 = R0 * K0.inv * Hxy.inv * K1                       | see Szeliski
   = R0 * K0.inv * (K * Ryx * K.inv) * K1
   = R0 * (K0.inv * K) * Ryx * (K.inv * K1)       | K0 = K1 = K
   = R0 * Ryx

Apparently I don't know whether Hxy = H01 or Hxy = H10. Intuitively I would assume the homography estimated is the one from the "from" camera to the "to" camera. So H01.inv would mean we are talking about R10. Continuing with the formula...

   = R0 * Rxy
   = R0 * R10                       | see Szeliski
   = R0 * R1 * R0.inv
   =? R1

Here's the problem. No matter how I look at it, I always end up questioning why R0 is multiplied from the left side and not the right side. Assuming Hxy = H10 does not solve the problem.

It would be great if anyone could review the formula and verify some of the assumptions I made. In particular

• Is pairwise_matches[pair_idx].H the homography from the view "from" to the view "to", or vice versa?
• Why is cameras[edge.from].R multiplied to the term from ...