One may take advantage of kernel separatibility to generate such Gaussian Kernel.
// mu: mean, sigma: standard deviation
float gaussianDistribution(float x, float mu, float sigma) {
return std::exp( -(((x-mu)/(sigma))*((x-mu)/(sigma)))/2.0 ) / (cv::sqrt(2 * CV_PI) * sigma);
}
cv::Mat_<float> getGaussianMask(int nrows, int ncols) {
cv::Mat_<float> gaussianMask = Mat_<float>::zeros(nrows, ncols);
// compute a bidimensional gaussian
for (int x = 0; x < gaussianMask.cols; ++x) {
for (int y = 0; y < gaussianMask.rows; ++y) {
// taking advantage of the gaussian's kernel separatibility
gaussianMask(y,x) =
gaussianDistribution(y, gaussianMask.rows/2 - 1, gaussianMask.rows/4 - 1) *
gaussianDistribution(x, gaussianMask.cols/2 - 1, gaussianMask.cols/4 - 1);
}
}
// normalizing
cv::Scalar totalsum;
totalsum = cv::sum(cv::sum(gaussianMask));
gaussianMask = gaussianMask.mul(1.0/totalsum[0]);
}
Resulting image for nrows = 128 and ncols = 64.
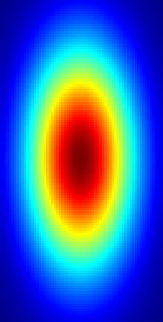
You may also vary the size of the standard deviation sigma to produce Gaussians with smaller or bigger radius. Here, I'm using gaussianMask.rows/4 and gaussianMask.cols/4. The mean mu determines the center of the Gaussian.
// ...
gaussianDistribution(y, gaussianMask.rows/2 - 1, gaussianMask.rows/4 - 1) *
gaussianDistribution(x, gaussianMask.cols/2 - 1, gaussianMask.cols/4 - 1);
I used cv::applyColorMap(gaussianMask, gaussianMask, cv::COLORMAP_JET); to get this coloring.

