The answer lies in the magic performed in the two middle rows of the projection equations involving x'' and y''. Assuming you have a camera that perfectly models the pinhole projection model, you could completely skip the x'' and y'' steps and just use the four equations involving x', y', u, and v. But this is not true of most (all?) cameras in practice. The camera's lens introduces distortion that deviates the projection of 3D scene points P = [X, Y, Z] from their ideal image coordinates (as predicted by the pinhole model) p = [u, v] to distorted coordinates p* = [u, v]. This effect varies depending on the quality of camera and the type of lens, typically points are warped away from the principal point proportional to their distance (positive radial distortion). The equations involving x'' and y'' are compensating the lens distortion, which must be done projecting the points onto the image plane. See Szeliski chapter 2.1.6 for more info.
EDIT: As to why distortion correction is (almost) always applied before projection on the image plane.
First, you are arguing about right and wrong, i.e. your proposed equations are right is right and OpenCV is wrong. This is not a fruitful way to look at the problem. Basically the pinhole camera model defines a set of conditions that any projection of a scene has to obey, the size of an object is inversely proportional to its distance to the camera, directly proportional to the focal length etc, directly related to its pose relative to the camera etc... Distortion correction is just a way of fitting an imperfect physical system fit into this ideal mathematical model, there is no one absolutely correct way it must be applied, as long it makes the imaging process closer to the pinhole camera model.
So yes you could perform distortion after projection on the image plane but before decentering, but this will require that your distortion function is estimated using image coordinates and not normalized camera coordinates. The distortion function is a non linear function without an explicit representation that is approximated via Taylor expansion up to 6th degree terms (depending on OpenCV flags), and it is dependent upon the coordinate system in which it was estimated. Because of this non linearity you cannot switch the order in which it is performed:
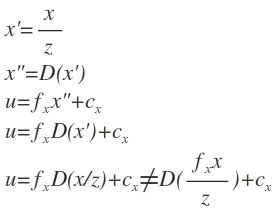
So if you want to use your projection equations you have to reestimate the distortion function in image coordinates.
Now there is a reason why distortion correction is typically performed as the OpenCV equations dictate, that is in normalized camera coordinates. Estimation of the distortion functions is performed during camera calibration where a planar pattern with a set of accurately known points is observed by the camera from many viewing angles and distances. Typically one of the first steps involves estimating the pose of the calibration target relative to the camera for each input image. Knowing the pose of the calibration pattern relative to the camera means you can ... (more)

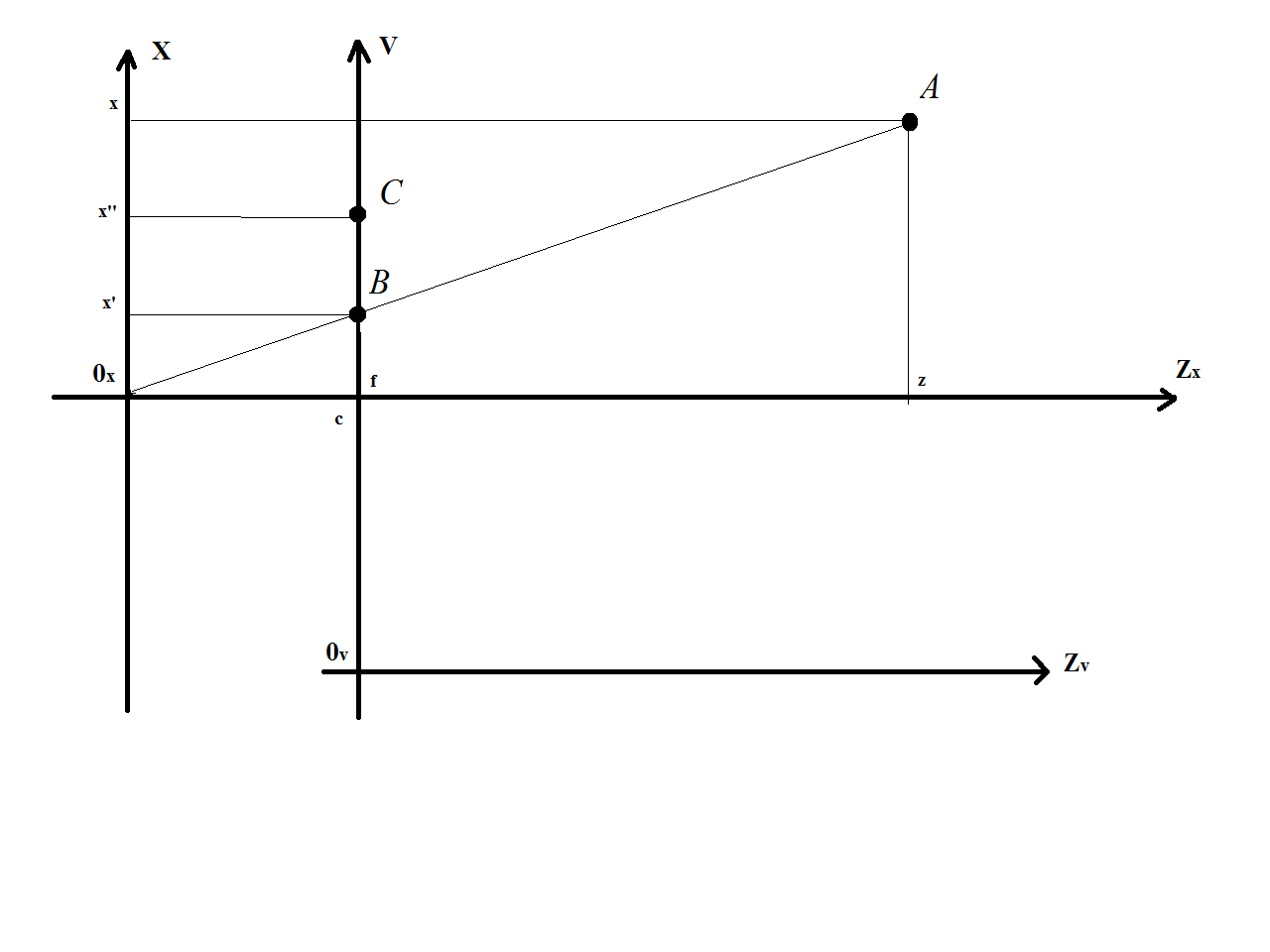

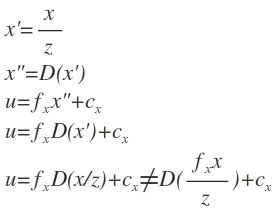
I have updated my answer to reflect your updated question.