Regarding the weights, I did some small tests to check the influence. Here are my results:
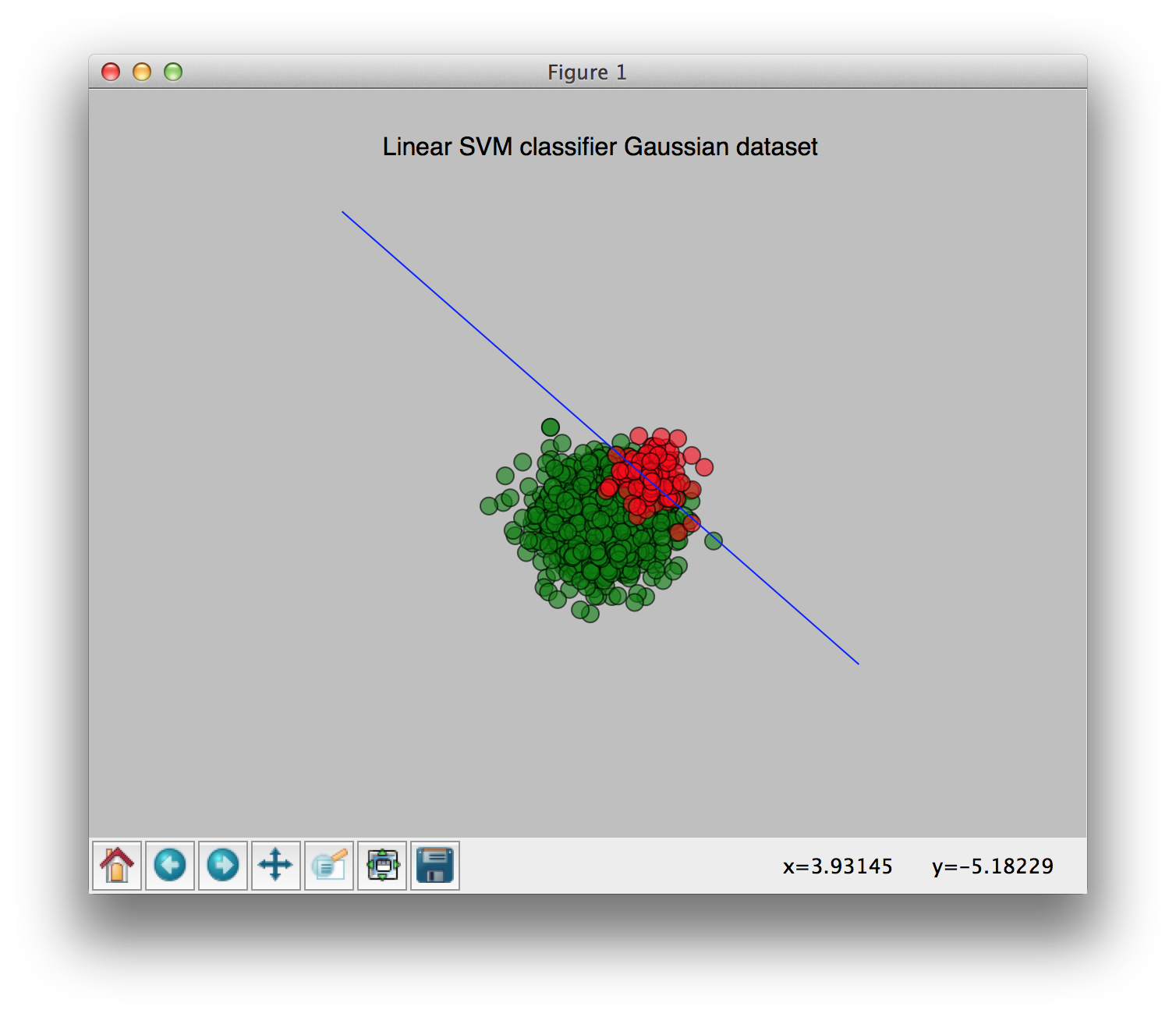
No weights:
With weights [0.9, 0.1] (0.9 for the largest class, 0.1 for the smallest class):
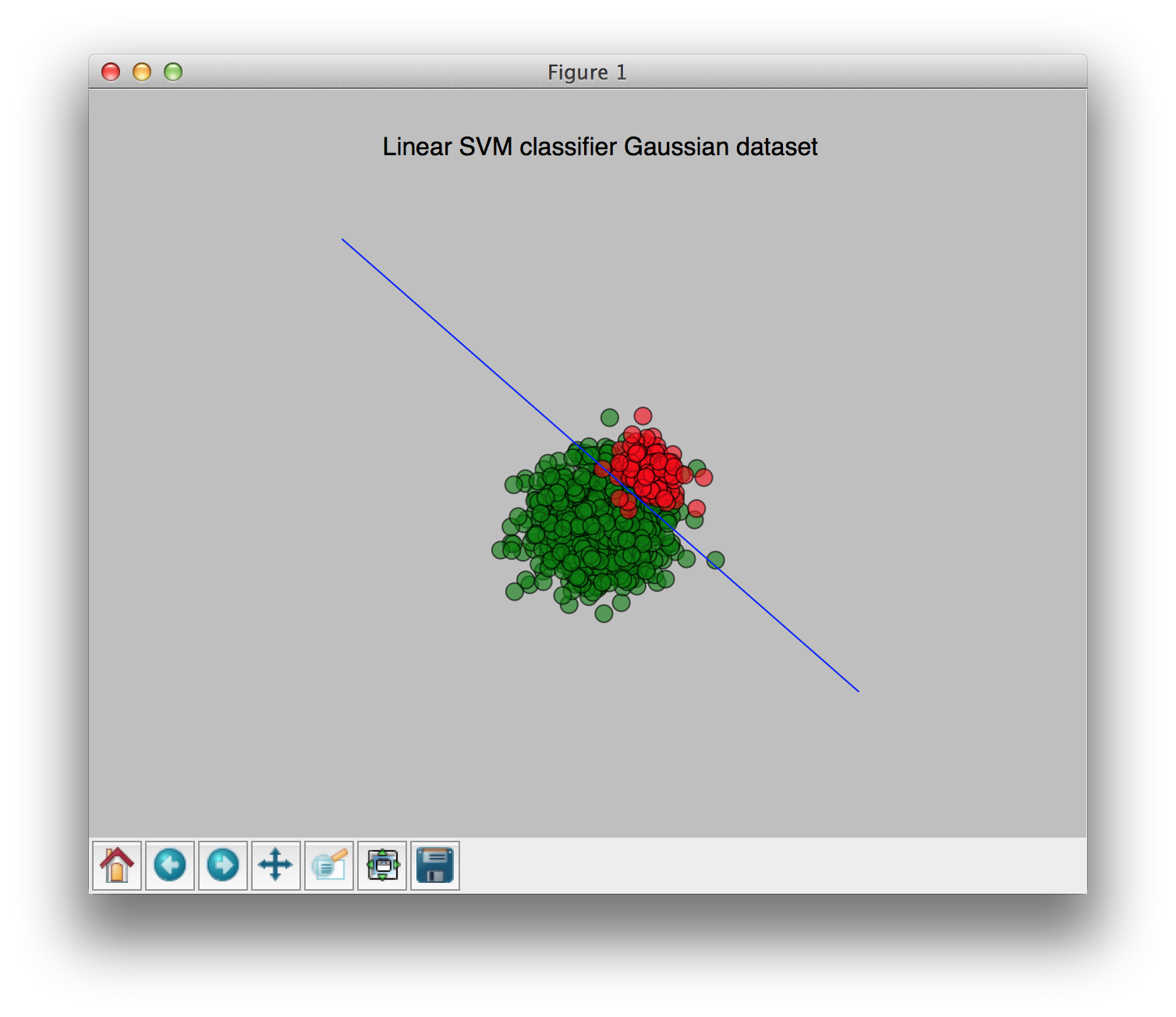
You can see the change of the weights clearly in these pictures. I hope this clears things up a bit.
On a side note: I tried to do this in python but the class_weights variable does not appear to get set properly (see this question for more information). To circumvent this I had hardcoded the weights in the opencv source, using c++ would've most likely given the correct results as well, as the weights seem to get properly set for c++.
Code used to generate the example:
import numpy as np
import cv2
import matplotlib.pyplot as plt
from os.path import isfile
import scipy.misc
import xml.dom.minidom
"""Originally from: http://stackoverflow.com/questions/8687885/python-opencv-svm-implementation"""
class StatModel(object):
"""parent class - starting point to add abstraction"""
def load(self, fn):
self.model.load(fn)
def save(self, fn):
self.model.save(fn)
"""Wrapper for OpenCV SimpleVectorMachine algorithm"""
class SVM(StatModel):
def __init__(self):
self.model = cv2.SVM()
def train(self, X, Y):
#setting algorithm parameters
params = dict( kernel_type = cv2.SVM_LINEAR,
svm_type = cv2.SVM_C_SVC,
C = 1,
class_weights = [0.9, 0.1],) # THIS DOES NOT WORK IN OPENCV PYTHON
self.model.train(X.astype(np.float32), Y.astype(np.float32), params = params)
# generates Gaussian dataset
def gen_gauss_dat(mu1, cov1, N1, mu2, cov2, N2):
X1 = np.random.multivariate_normal(mu1, cov1, (N1))
X2 = np.random.multivariate_normal(mu2, cov2, (N2))
X = np.vstack([X1,X2])
Y = np.hstack([np.ones((X1.shape[0]))*-1, np.ones((X2.shape[0]))])
return X, Y
def load_model(path):
if path == None:
return None
if isfile(path) == False:
return None
print "Loading model from {}".format(path)
model = xml.dom.minidom.parse(path)
# TODO: handle multiple support vectors?
weights = np.fromstring(model.getElementsByTagName("_")[0].childNodes[0].nodeValue, sep=" ")
alpha = float(model.getElementsByTagName("alpha")[0].childNodes[0].nodeValue)
rho = float(model.getElementsByTagName("rho")[0].childNodes[0].nodeValue)
weights = weights * -alpha
return weights, rho
# generate Gaussian data
X, Y = gen_gauss_dat([0,0], np.identity(2)*1.5, 1000, [2,2], np.identity(2) * 0.5, 100)
# train on the generated Gaussian data
svm = SVM()
svm.train(X, Y)
svm.save("svm.xml")
w, b = load_model("svm.xml", )
# plot the data
plt.scatter(X[Y==-1,0],X[Y==-1,1], c="g", alpha=0.6, s=100)
plt.scatter(X[Y==1,0],X[Y==1,1], c="r", alpha=0.6, s=100)
x = [-10, 10]
y = [(-w[0] * x[0] - b) / w[1], \
(-w[0] * x[1] - b) / w[1]]
plt.plot(x, y)
plt.axis("off")
plt.title("Linear SVM classifier Gaussian dataset")
plt.show()






Never used SVM so I can't really help you there, but please post your conclusions when you finish this study. Good luck. I can refer you to this study by Piotr Dollar https://www.google.pt/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=0CEIQFjAC&url=https%3A%2F%2Fs3-us-west-2.amazonaws.com%2Fmlsurveys%2F97.pdf&ei=IP3fUr-hFsSX1AX26YC4Bg&usg=AFQjCNEHJ_cBNqOAmMV_GE4q6plvpmmveA&sig2=BLIfURmlWm4u_33KLLJbRg&bvm=bv.59568121,d.bGQ&cad=rja where he compares the performance of various detectors on multiple pedestrian datasets, among them the SVM HOG and VJ algorithms. It is a pretty good evaluation.
I know of the work of Dollár which is one of the main paper resources I am using for my own research :) I have succesfully created a wrapper around the output of the CvSVM training to create an output that can be used by the HOGDescriptor interface. Master branch even got a recently merged version for that done by @Mathieu Burchanon. However, as many of the ML functionality in OpenCV, the parameter tuning and study is enourmous :) I will see how far I get, feel free to contact me from time to time to ask about progress!