arclength and contourarea wrong results?
I am using cv2's arclength and contourarea in my python project. To verify the results I've applied both functions to a discretized circle with r=100. The circumference of the circle should be around pi2100 = 628,31 and the area should be approximatly pi*100^2=31415.92.
Getting the circumference and area using cv2:
import numpy as np
import cv2
canvas = np.zeros((500, 500), dtype=np.uint8)
circle = cv2.circle(canvas, (250, 250) , 100, 10, -1)
contours, hierarchy = cv2.findContours(circle, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
for cnt in contours:
circumference = cv2.arcLength(cnt, True)
area = cv2.contourArea(cnt)
print("c: %s" % circumference)
print("area: %s" % area)
I would expect the estimations to be close to the theoretical value but it returns circumference=661.75 and area=31134, which both have quite a big error.
I've also estimated the area by simply counting the non-zero pixels:
area_nzp = np.count_nonzero(circle)
print(area_nzp)
Which returns area=31417, being much closer to the theoretical value.
I was wondering if anyone could tell me how to use arclength and contourarea in the "correct way" such that the error will become smaller. Thanks in advance.
Edit: Inspired by LBerger's comment I plotted the error between the error of theoretical surface value of the circle vs ContourArea and the area estimated by counting the non-zero pixels. I do not understand why ContourArea's error can be this big. Does anyone know what actually happens when the function is run?


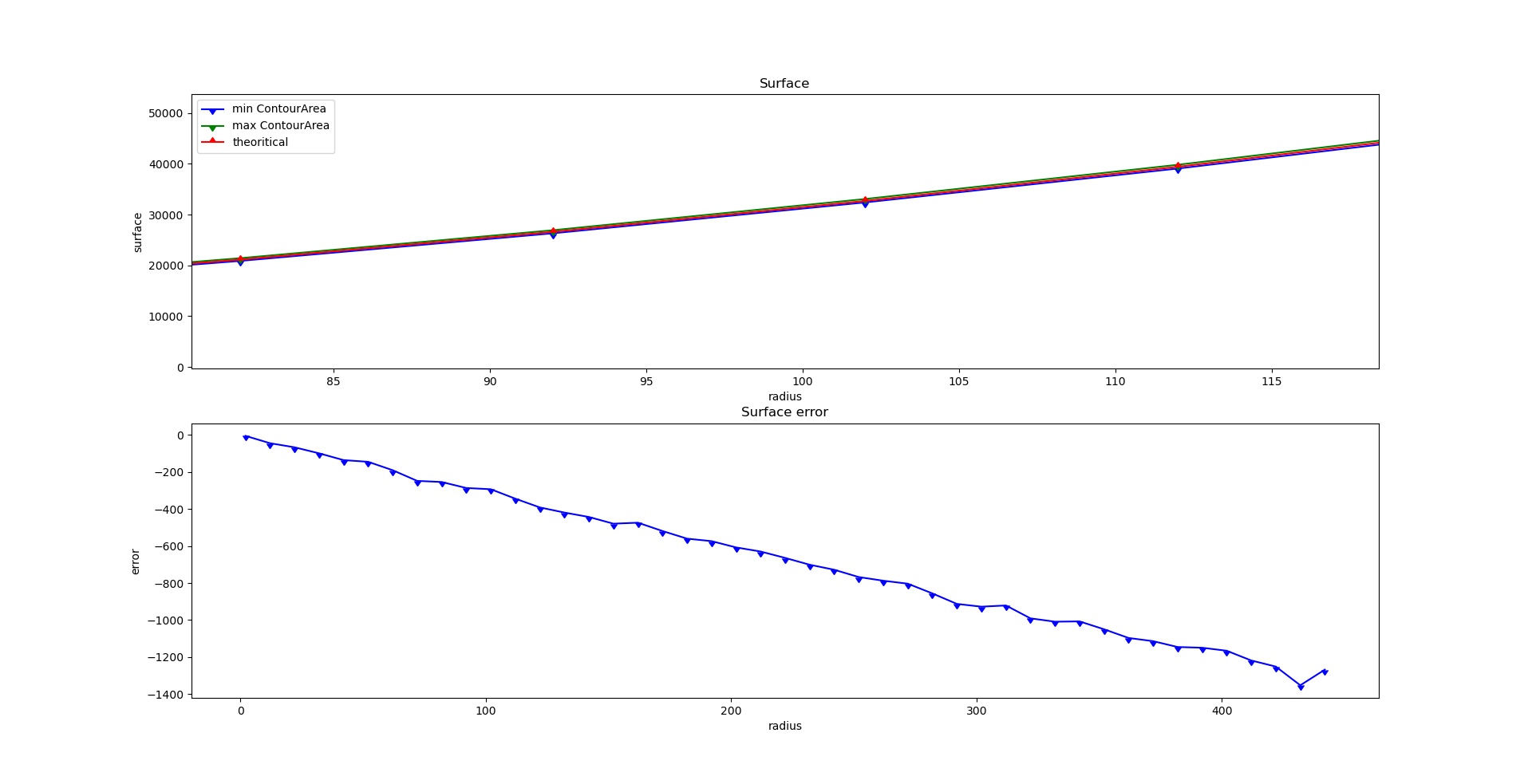 You can estimate surface error using perimeter
You can estimate surface error using perimeter
your circle is not an ideal one, but a bresenham approximation
try it with a rectangle, and it'll be exact
also, cv2.CHAIN_APPROX_SIMPLE
Thanks for your comment. The circle is not ideal but don't you agree that the error is too big? Especially in comparison with the estimation of the area by counting the non-zero pixels