3D points from Reprojection Q Matrix
Hello everyone,
I have been working with the reprojection matrix [Q] in a stereo configuration to get 3D coordinates from a 2D image. The [Q] matrix is described as :
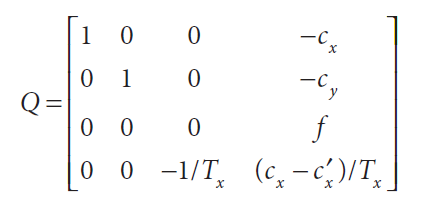
To get 3D points from 2D points in an image, I should be able to use this matrix as follows :
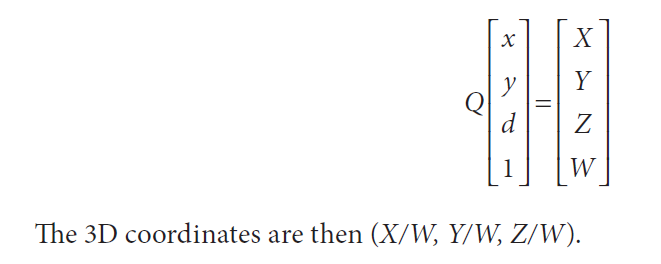
By doing the matrix multiplication, I get the 3 following formulas for x, y and z coordinates in 3D :
- x_3D = (x_pixel - Cx) / (-1/Tx * d)
- y_3D = (y_pixel - Cy) / (-1/Tx * d)
z_3D = f / (-1/Tx * d)
where x_pixel and y_pixel are the x and y position of the point in the image, Tx is the distance between my 2 cameras and d is the disparity.
However, if I look on the internet for triangulation formulas to express XYZ coordinates from a 2D image, I can only find the formula I found for the z coordinate. For x and y coordinates, I do not find a similar formula, here is what I found :
- x_3D = x_pixel * z_3D / f
- y_3D = y_pixel * z_3D / f
What is the relation between the formulas given using the Q matrix, where Cx, Cy and Tx appear and the formulas given for the triangulation ?
Thank you.

You can have a look at this book for more information.
Thank you for your reply. Unfortunately, I have already been working with this booking, and it is exactly from there that I found the expressions in the images above... But I don't understand why the cx, the cy and the Tx appear in these formulas when doing the matrix multiplication ...