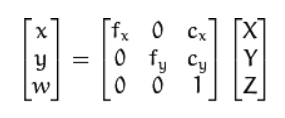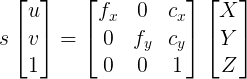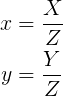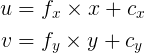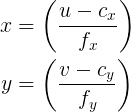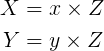is it possible to calculate a points 3D X and Y coordinate by inverting camera matrix

asked 2019-01-19 02:15:12 -0600

mikeitexpert
1 ●2 ●5

updated 2019-01-19 03:25:30 -0600

LBerger
9317 ●2 ●20 ●88 http://www.traimaocv.fr

I have read camera calibration explained.

I was able to do it with and just to test it i used this and everything is perfectly working.

I am just curious given the below equation and assuming I know the Z of a 3D point and its x,y pixel coordinates in the image, would I be able to assess the X, and Y coordinates of the 3D point?

In other words if I multiple the two sides of the equation by inv of camera matrix, and assuming I know the Z = w of a 3D point, then can I get the 3D X and Y of the point in 3D space?

![image description] (https://docs.opencv.org/2.4/_images/m...)

Any comments is much appreciate it. $C:\fakepath\Selection_007.png$

answered 2019-01-19 05:45:51 -0600

Eduardo
3589 ●1 ●15 ●41

Yes you can. No need to invert the camera intrinsics matrix.

Perspective projection equations:

eq1

eq2

eq3

Reverse perspective projection equations assuming a known Z:

eq4

eq5

edit flag offensive delete link

Comments

Thank you for valuable comment

I was wondering how would a small error in measurement of Z would distort the X and Y values assuming the is no error in measuring u and v.

Would you confirm it correlates with 1 / fx and 1/fy for X and Y direction? For my case it would be approximately 1/200.

I guess what I am trying to say is that the higher the fx and fy the lower detect we would experience from measuring Z/depth. Or simply the higher the resolution the more error we can tolerate introduced by measuring Z.

I hope it doesn't sound confusing. :)

Please let me know.

Regards

mikeitexpert ( 2019-01-19 11:56:50 -0600 )edit

add a comment

is it possible to calculate a points 3D X and Y coordinate by inverting camera matrix

1 answer

Comments

Links

Question Tools

Stats

Related questions

is it possible to calculate a points 3D X and Y coordinate by inverting camera matrix edit

1 answer

Comments

Links

Question Tools

Stats

Related questions

is it possible to calculate a points 3D X and Y coordinate by inverting camera matrix