Extract rotation and translation from Fundamental matrix
Hello,
I try to extract rotation and translation from my simulated data. I use simulated large fisheye data.
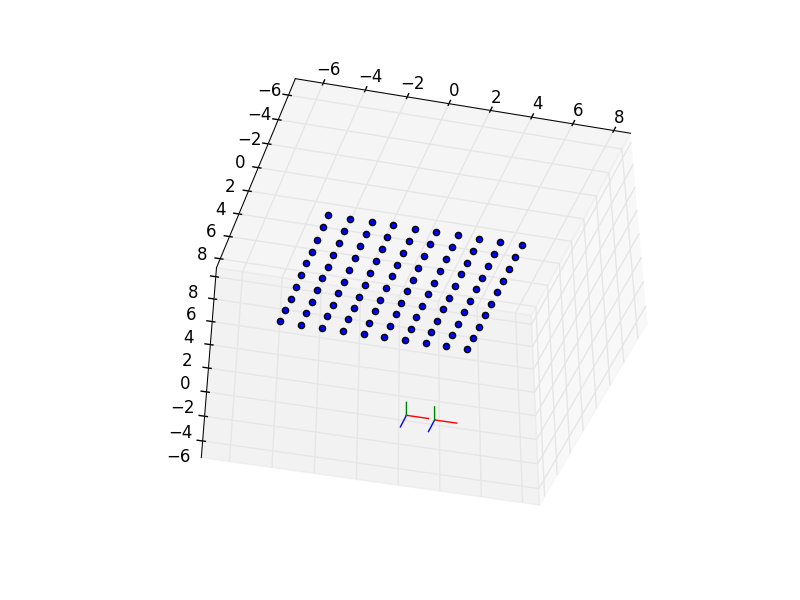
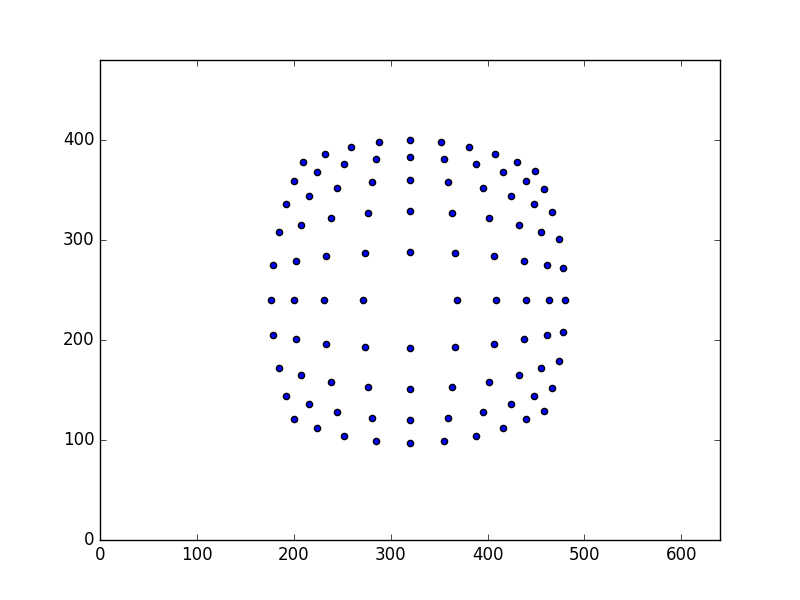
So I calculate my fundamental matrix : fundamentalMatrix [[ 6.14113278e-13 -3.94878503e-05 4.77387412e-03] [ 3.94878489e-05 -4.42888577e-13 -9.78340822e-03] [-7.11839447e-03 6.31652818e-03 1.00000000e+00]]
But when I extract with recoverPose the rotation and translation I get wrong data:
R = [[ 0.60390422, 0.28204674, -0.74548597], [ 0.66319708, 0.34099148, 0.66625405], [ 0.44211914, -0.89675774, 0.01887361]]),
T = ([[0.66371609], [0.74797309], [0.00414923]])
Even when I plot the epipolar lines with the fundamental matrix the lines don't fit the corresponding point in the next image.
I don't really understand what I do wrong.
fundamentalMatrix, status = cv2.findFundamentalMat(uv_cam1, uv_cam2,cv2.FM_RANSAC, 3, 0.8) cameraMatrix = np.eye(3); i= cv2.recoverPose(fundamentalMatrix, uv_cam1, uv_cam2, cameraMatrix)



