Measuring a Cube without depth

edit

I'm trying to measure a cube without depth. I have the following information

A plane that is position at 0,0,0 with normal up (0,1,0) Detected corners of the cube, I choose them using the click of the points. I convert the points into 3D using the inverse of camera matrix at Z = 1 Then I do line plane intersection to get 3D Positions of the clicked points. My problems 1. How do I correctly visualize the results, right now I'm trying to visualize a plane, but it's always centered at camera position 2. Is the process correct ? Is there are any other steps that I need to do ? 4. Giving camera position and orientation, How is that useful ?

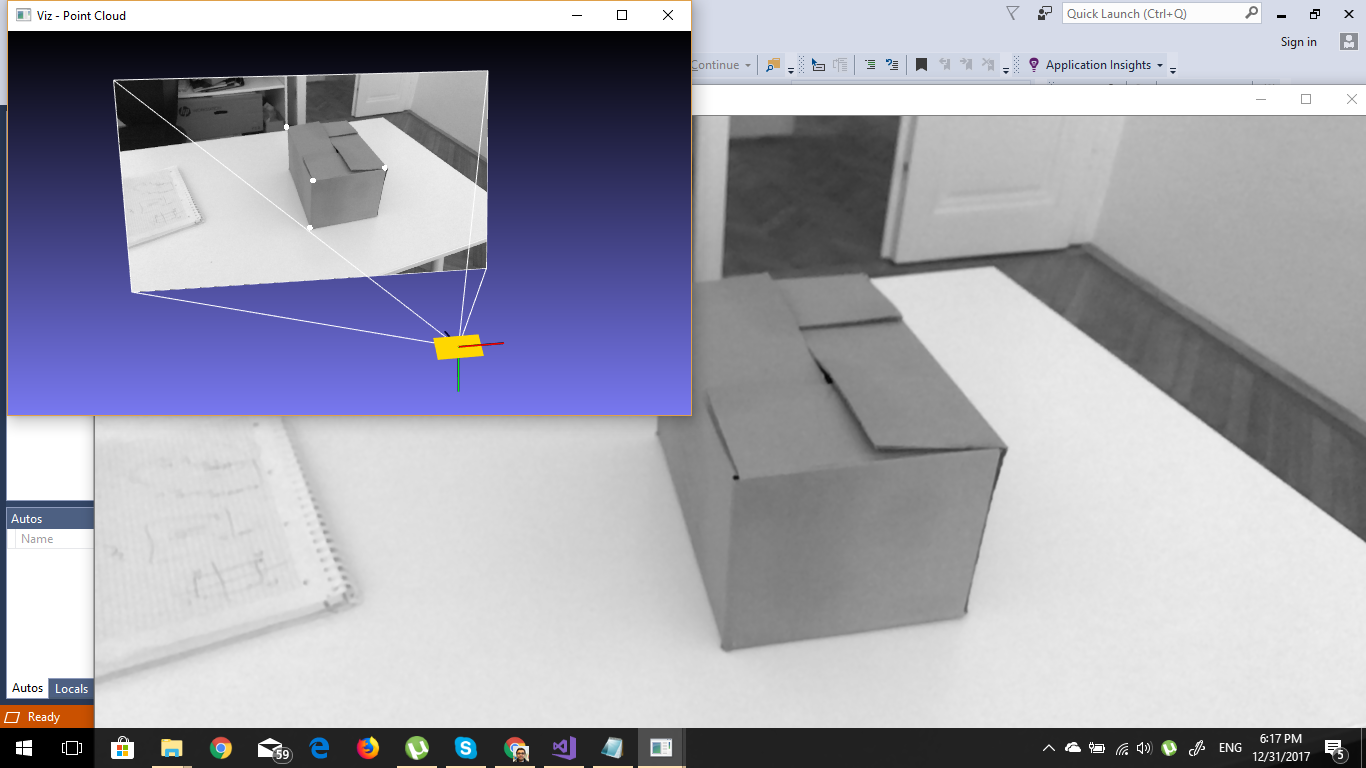
Here is the picture progress so far

    //Generate a camera intrinsic matrix
        cv::Matx33d K;
        K<< 1700, 0, src.cols / 2,
            0, 1700, src.rows / 2,
            0, 0, 1;



        std::vector<cv::Vec3d> pointsTransformed3D;


        Mat Pose = (Mat_<double>(3, 4)
            << 1, 0, 0, 0,
            0, 1, 0, 0,
            0, 0, 1, 0);

        Mat H = (Mat_<double>(3,3));
        Mat transposePose = (Mat_<double>(3, 3));

        //transpose(Pose, transposePose);

        //H = K*transposePose;


        std::vector<cv::Vec3d> points3D;
        for (int i = 0; i < corners.size(); i++)
        {
            cv::Vec3d pt;

            pt[2] = 1.0f;

            pt[0] = (corners[i].x);
            pt[1] = (corners[i].y);

            points3D.push_back(pt);
        }

        cv::transform(points3D, pointsTransformed3D, Pose);

        std::vector<cv::Vec3d> points3DProjected;
        cv::transform(pointsTransformed3D, points3DProjected, K.inv());


        for (int i = 0; i < points3DProjected.size(); i++)
        {

            points3DProjected[i][0] = points3DProjected[i][0] / points3DProjected[i][2];
            points3DProjected[i][1] = points3DProjected[i][1] / points3DProjected[i][2];
            points3DProjected[i][2] = points3DProjected[i][2] / points3DProjected[i][2];
        }









    Mat rot = (Mat_<double>(3, 3)
                << 1, 0, 0,
                0, 1, 0,
                0, 0, 1);

            Mat translVec(3, 1, CV_64F);
            translVec.at<double>(0, 0) = 0;
            translVec.at<double>(1, 0) = 0;
            translVec.at<double>(2, 0) = 0;


            std::vector<Ray> rays;
            for (int i = 0; i < points3DProjected.size(); i++)
            {

                Ray ray;

                ray.origin = Vec3f(translVec.at<double>(0, 0), translVec.at<double>(1, 0),
                    translVec.at<double>(2, 0));
                ray.direction = Vec3f(points3DProjected[i][0] - translVec.at<double>(0, 0),
                    points3DProjected[i][1] - translVec.at<double>(1, 0), points3DProjected[i][2] - translVec.at<double>(2, 0));
                ray.direction = normalize(ray.direction);
                rays.push_back(ray);
            }
            std::vector<cv::Vec3f> contacts;

            for (int i = 0; i < points3DProjected.size(); i++)
            {
                Vec3f pt(0, 0, 0);

                cv::Vec3f contact;
                std::pair<bool, double> test = linePlaneIntersection(rays[i].direction, rays[i].origin, Vec3f(0, 1, 0), pt);
                if (test.first == true)
                {
                    cv::Vec3f contact(rays[i].origin + (rays[i].direction) * test.second);
                    contacts.push_back(contact);
                }
            }


            //Project the 3D Point onto 2D plane
            std::vector<cv::Point2d> points_2d;
            std::vector<cv::Point3d> points_3d;
            std::vector<cv::Point3d> lines_3d;
            std::vector<cv::Point2d> lines_2d;
            for (int i = 0; i < points3DProjected.size(); i++)
            {
                cv::Point3d pt;
                pt.x = (points3DProjected[i][0]);
                pt.y = (points3DProjected[i][1]);
                pt.z = (points3DProjected[i][2]);
                points_3d.push_back(pt);
            }




            // Create zero distortion
            cv::Mat distCoeffs(4, 1, cv::DataType<double>::type);
            distCoeffs.at<double>(0) = 0;
            distCoeffs.at<double>(1) = 0;
            distCoeffs ...