Projection matrices in OpenCV vs Multiple View Geometry
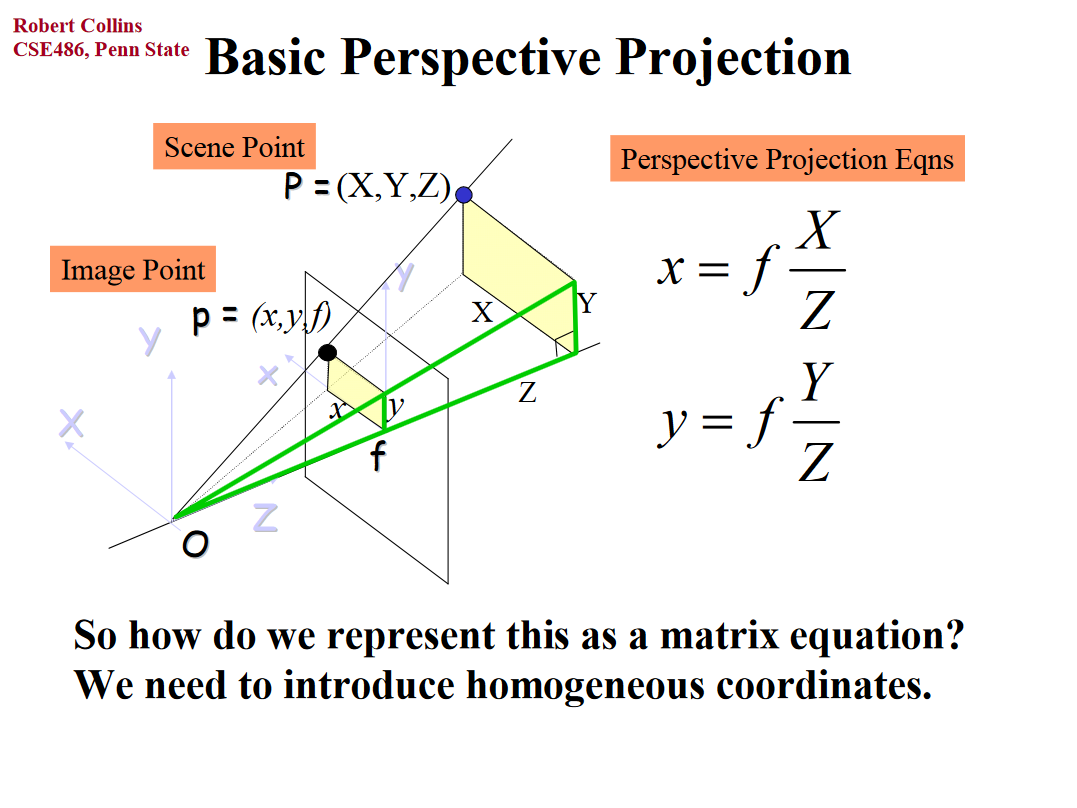
I am trying to follow "Multiple View Geometry in Computer Vision" formula 13.2 for computing the homography between for a calibrated stereo rig. It should be simple math
H = K' (R - t. transpose(n) / d) inv(K)
Where H is the 3x3 homography. K and K' are 3x3 camera intrinsic matrices, R is a 3x3 rotation between the cameras. t is column vector translation between the cameras. n is a plane normal vector and d is the constant of the plane equation of a plane that both cameras are viewing. The idea here is that going right to left, a homogenous pixel coordinate is unprojected to a ray, the ray is intersected with a plane and the intersection point is projected to the other image.
When I plug numbers in and try to match up two captured images I can't get the math as shown to work. My main problem is that I don't understand how simply multiplying a 3D point by a camera matrix K can project the point. In the opencv documentation for the calibration module:
x' = x / z
y' = y / z
u = fx * x' + cx
v = fy * y' + cy
By the above math, x and y are divided by z before the focal length is multiplied. But I don't see how the math from the text accomplishes the same thing by merely multiplying a point by K. Where is the divide by z in the formula for H?
Can someone help with this problem that is probably just notation? Scott