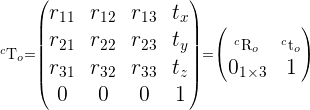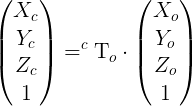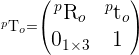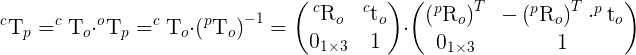calibrate stereo system without calling cv::stereoCalibrate
I saw a program to calibrate a stereo system (Camera-projector pair). The output of the program is :
- camera intrinsic matrix
- camera distortion coefficients
- camera extrinsic vectors (Obtained by
rvecsandtvecsofcv::calibrateCamera) - projector intrinsic matrix
- projector distortion coefficients
- projector extrinsic vectors (Obtained by
rvecsandtvecsofcv::calibrateCamera)
I digged into the code and there was no calling for cv::stereoCalibrate. However, the program uses those 6 outputs to scan 3D objects successfully (the source of the scanning is closed, I have just the calibration part).
How is this possible? How can I achieve rotation matrix and translation vector in order to get the essential matrix from rvecs and tvecs ? What I missing here?