I do not understand the difference between these two equations:
1. from wikipedia:
https://en.wikipedia.org/wiki/Rodrigu...
2. from open CV doc:
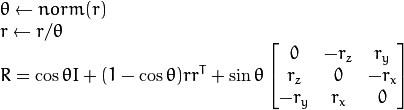
http://docs.opencv.org/2.4/modules/ca...
Where is the cos(θ) gone on the wiki page in the formula 1. ?
Shouln't it be: v_{rot} = cos(θ)v + sin.... ?
Then on the wiki page, there is no more cos(θ) in the definition of R...
Or did I miss something?
I think the relevant bit is up the page a bit. In the Statement section. There you see exactly the equation you ask about.
yes but it's also consistent with what is down the page :
https://wikimedia.org/api/rest_v1/med... so there is no cos(θ)...
Looking at HERE, still a cos involved. Not sure what the Matrix Notation there represents, but that's definitely not the formula you use.
Anyway, in the 'talk' page on wiki ( https://en.wikipedia.org/wiki/Talk:Ro... ), one can read an interesting thins under "Error in formula?"... that I absolutely do not understand by the way... There must be some tweak or whatever, but I also saw this formula without the cos(θ) for the rotation matrix definition.
Like I said, I'm not sure what it is representing, but it is not the same thing and cannot be substituted. K (capital) is very much not the same as k (not capital). It may look similar, but if you use it without understanding, you'll use it wrong.
Specifically, K^2 v = k cross (k cross v), but the top equation has k (k dot v) in the third term.
K is the cross-product equivalent matrix form of the vector k. So said, you can apply (simple matricial product) K to a vector v, it would give exactly the same result as a vectorial cross product between k and your vector v.
Asked: 2017-07-02 16:47:32 -0600
Seen: 1,549 times
Last updated: Jul 02 '17
