Angles in ellipse() function
Hi,
I am trying to draw an ellipse using OpenCV. But I have difficulty in understanding its angle arguments. Even it is not clear from the picture in OpenCV docs.
I tried following line:
cv2.ellipse(img,(256,256),(200,100),0,90,180,(0,0,255),4,cv2.CV_AA)
I got the result as below:
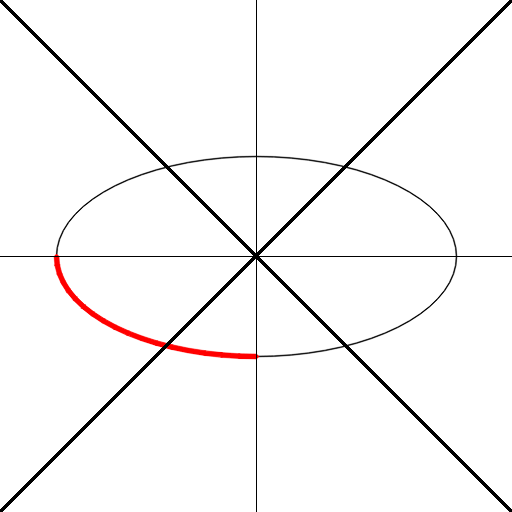
That means startangle is taken from positive x axis in clockwise direction and that is same for endangle.
Now I tried this :
cv2.ellipse(img,(256,256),(200,100),0,45,225,(0,0,255),4,cv2.CV_AA)
I got the output as below :

See, the startangle and endangle is not 45 and 225 here.
What is the problem here? Did I miss something ? Or is it a bug?

