StereoRectify with very different camera orientations

edit

This is a recap for this question.

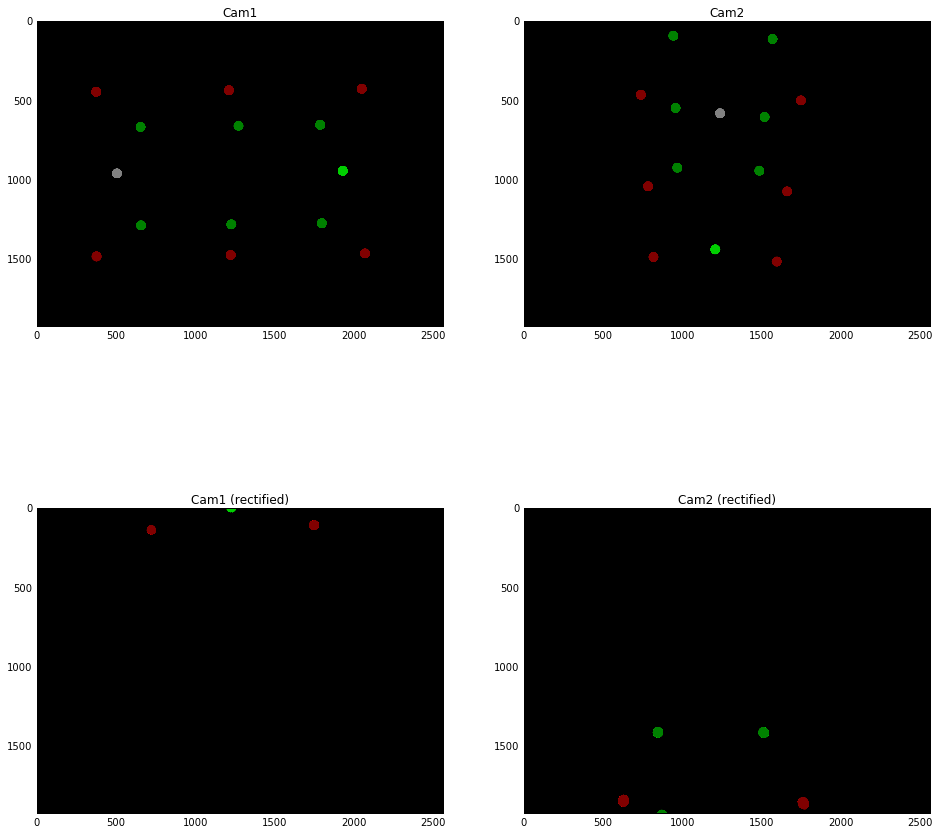
I have a camera setup where two cameras are positioned in very different orientations. I managed to rectify the images but the content is transformed out of the image. I believe that the reason for this is that the principal points of the rectified image are set to quite awkward positions after rectification.

I got several questions now:

• Is it save to change the principle points of either projection matrix to center the content of the rectified image?
• How do I get the full projection matrix from world coordinates to rectified image for either camera given:
  • Original rotation matrix of Camera
  • Rectified rotation matrix of Camera (calculated by stereoRectifiy)
  • Intrinsic parameters of Camera
  • Translation vector in Camera Coordinates
  • rectified Projection matrix (calculated by stereoRectifiy)
• Is there a best-practice of how to deal with Camera setups with very different camera orientations?

Code:

import matplotlib.pyplot as plt
import cv2
import numpy as np

# =============================================
# Helper Functions
#     not relevant to understand the problem
# =============================================

def project_3d_to_2d(Cam, points3d):
    """
    This is a 'dummy' function to create the image for
    the rectification/stereo-calibration.
    """
    R = Cam['R']
    pos = Cam['pos']
    K = Cam['K'].astype('float32')

    # pos to tvec
    tvec = np.expand_dims(
        np.linalg.inv(-np.transpose(R)) @ pos,
        axis=1
    ).astype('float64')

    # rot to rvec
    rvec = cv2.Rodrigues(R)[0].astype('float64')

    points2d, _ = cv2.projectPoints(
        np.array(points3d), rvec, tvec, K, 0)
    return np.ndarray.squeeze(points2d).astype('float32')

def img(Cam, points3d):
    """
    Creates the 'photo' taken from a camera
    """
    W = 2560
    H = 1920
    Size = (W,H)

    points2d = project_3d_to_2d(Cam, points3d)

    I = np.zeros((H,W,3), "int8")

    for i, p in enumerate(points2d):
        color = (0, 50, 0)
        if i == 1:
            color = (255, 255, 255)
        elif i > 1 and i < 8:
            color = (255, 0, 0)
        elif i >= 8:
            color = (0, 255, 0)

        center = (int(p[0]), int(p[1]))
        cv2.circle(I, center, 32, color, -1)

    return I

# =============================================
# Cameras
# =============================================

Cam1 = {
    'pos': np.array(
        [72.5607048220662, 381.44099049969805, 43.382114809969224]),
    'K': np.array([
        [-3765.698429142333, 0.0000000000002, 1240.0306479725434],\
        [0, -3765.6984291423264, 887.4632405702351],\
        [0, 0, 1]]),
    'R': np.array([
            [0.9999370140766937, -0.011183065596097623, 0.0009523251859989448],\
            [0.001403670192465846, 0.04042146114315272, -0.999181732813928],\
            [0.011135420484979138, 0.9991201351804128, 0.04043461249593852]
        ]).T
}

Cam2 = {
    'pos': np.array(
        [315.5827337916895, 325.6710837143909, 50.172023537483994]),
    'K': np.array([
        [-3680.6894379194728, 0.000000000006, 1172.8022801685916],\
        [0, -3680.689437919353, 844.1378056931399],\
        [0, 0, 1]]),
    'R': np.array([
        [-0.016444826412680857, 0.7399455721809343, -0.6724657001617901],\
        [0.034691990397870555, -0.6717294370584418, -0.7399838033304401],\
        [-0.9992627449707563, -0.03549807880687472, -0.014623710696333836]]).T
}

# =============================================
# Test rig
# =============================================

calib_A = np.array([20.0, 90.0, 50.0])  # Light-Green
calib_B = np.array([130.0, 90.0, 50.0])  # White

calib_C = np.array([  # Red
    (10.0, 90.0, 10.0),
    (75.0, 90.0, 10.0),
    (140.0, 90.0, 10.0),
    (140.0, 90.0, 90.0),
    (75.0, 90.0, 90.0),
    (10.0, 90.0, 90.0)
])

calib_D = np.array([  # Green
    (20.0, 16.0, 20.0),
    (75.0, 16.0, 20.0),
    (130.0, 16.0 ...